img021

PRACA I ENERGIA

PRACA I ENERGIA

,

; \56.ijWyznaczyć pracę wciągnięcia ciężaru po równi pochyłej, jeśli masa tego ciężaru wynosi lOOkg, długość równi - 2m, kąt nachylenia do poziomu - 30°, współczynnik tarcia - 0.1. Przyjmij, że przyspieszenie ziemskie g = 9.8 m/s².

Zakładamy, że ciężar był wciągany ze stałą prędkością. Wtenczas siły działające na rozważane ciało w kierunku ruchu muszą się równoważyć. Prowadzi to do następującego równania:

F-P, +T

Przy czym P] jest składową siły ciężkości działającą stycznie do powierzchni równi (siła zsuwająca): Pl = Psina = mg sin a, natomiast T jest siłą tarcia, która jest równa T = fPi, gdzie f jest współczynnikiem tarcia, a P₂ = mg cos a jest siłą nacisku.

Tak więc:

F- mg sm a+ mgf cos a = mg(sina +/cosa). Wartość szukanej pracy wynosi W = Fs a zatem:    (T-=mgj(sina+/cosa)

i podstawiając dane W = 3413 J.

. Ciało o masie m wciągnięto powoli na górkę, działając siłą F, która w każdym punkcie była styczna do stoku górki (rysunek). Znaleźć pracę tej siły, jeśli wysokość górki wynosi h, jej długość /, a współczynnik tarcia/.

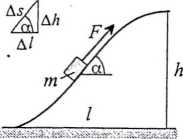
Z treści zadania wynika, że siła F działająca na ciało nie nadaje mu przyspieszenia, a jedynie równoważy składową siły ciężkości równą mg sin a oraz siłę tarcia równą fmgcos a, gdzie a jest kątem nachylenia stoku na danej wysokości. Elementarna praca siły F na drodze Aswynosi

AW = FAs = (wgsin a + fmg cos a)As Zauważmy, że

As sin a = AA - elementarna zmiana wysokości

Stąd

As cos a = A/ - elementarna zmiana długości A W = mgAh + fmg Al.

Praca całkowita jest sumą prac elementarnych wykonanych przy wciąganiu ciała od podnóża górki na jej wierzchołek:

W= 2 AW - mg JAA + fmg 2 A / = mgh + mgl.

Jak widać niezależnie od tego jaki jest kształt górki całkowita praca W zależy jedynie od jej wysokości oraz długości.

zsuwa się po powierzchni nachylonej pod kątem a do poziomu. 'Współczynnik tarcia k zależy od przebytej drogi przez ciało s i k(s)= bs, gdzie b jest dodatnim współczynnikiem. Wyznaczyć drogę sx przebytą przez ciało do momentu zatrzymania się oraz maksymalną prędkość ciała na drodze sj.

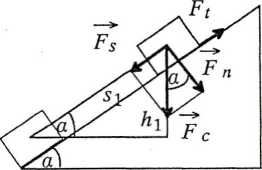
Na ciało zsuwające się po nachylonej powierzchni (równi pochyłej) działa siła ciężkości F_c = mg oraz siła tarcia F_t. Rozłóżmy siłę ciężkości na dwie składowe - składową F_s równoległą do równi i składową F_n prostopadłą do równi. Z rysunku widać, że Fs = mg sin a oraz F_n = mg cos a.

Z definicji siły tarcia F_t = kF_n otrzymujemy zatem F_c = kmgcosa. Ponieważ współczynnik tarcia k zależy od przebytej drogi s (k(s)=bs) więc siła tarcia też jest funkcją tej drogi F,(s) = bmg cos a s

Aby rozwiązać zadanie skorzystamy z zasady zachowania energii. Energia potencjalna na początku ruchu E_p = mgh\ (h\jest różnicą poziomów między położeniem początkowym a końcowym ciała) zostaje w całości zużyta na pracę przeciwko sile tarcia W na drodze sj, czyli do momentu zatrzymania się, gdyż w chwili zatrzymania się ciała energia kinetyczna £^. = 0. Ponieważ siła F_t zmienia się w czasie ruchu więc korzystając z definicji pracy otrzymujemy

* j F_t(s)ós.

si

bmgcosa j sds = -^bmgcosa

Podstawiając Ft(s)dostajemy W =

Porównując E_p z otrzymaną pracą mamy

mgs\ sina = jbmgcosa s\, gdzie skorzystaliśmy z zależności

hi = sj sin a.

Po przekształceniach otrzymujemy

2taa

Wyznaczmy zależność prędkości v ruchu ciała od przebytej drogi s. W dowolnej chwili ruchu energia kinetyczna jest równa różnicy początkowej energii potencjalnej i pracy przeciwko sile tarcia

E_k = E_p-W

Otrzymujemy zatem zależność

— mgs sin a - jbmg cos a s²,

gdzie ostatni człon równania jest tym razem pracą wykonaną po przebyciu drogi s. Stąd

v_s = Jlgs sin a - gb cos a s² .

59