img041 (38)

46

Oznacza to pominięcie we wzorze Taylora (3.36) składnika reszty r(pc, x₀), jako zaniedby-walnie małego w porównaniu z sumą pierwszych dwóch składników wzoru.

Z geometrycznego punktu widzenia odpowiada to aproksymacji wykresu funkcji/(O styczną poprowadzoną do wykresu w punkcie (x₀,/(*o)) (zob. rys. 3.5).

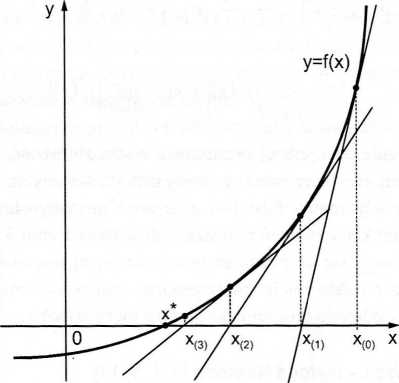
Rys. 3.5. Konstrukcja ciągu kolejnych przybliżeń w metodzie stycznych

Krok 1 algorytmu stycznych

Równanie (3.1) zastępowane jest równaniem aproksymującym

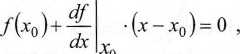
-o

(3.39)

którego rozwiązaniem jest

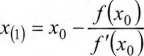
(3.40)

(liczbę x₍i) otrzymuje się rozwiązując równanie (3.39) ze względu na x). Z geometrycznego punktu widzenia x₍₁) jest współrzędną punktu przecięcia stycznej poprowadzonej do wykresu funkcji/(-) w punkcie (x₀,J[xo)) z osią Ox (zob. rys. 3.5).

tomiast/(X(i)) * 0, to sprawdza się, czy spełnione są warunki I /(x₍₁₎) | < 8 i I x₍p - x₀1 < £,

Jeżeli y(x₍₁₎) = 0, to x_(J) jest jednym z pierwiastków danego równania (3.1). Jeżeli na-

gdzie 8 i s są danymi liczbami dodatnimi określającymi dokładność wyznaczenia pierwiastka. Jeżeli warunki te są spełnione, to otrzymana liczba x₍₁₎ jest przyjmowana jako przybliżona wartość pewnego pierwiastka danego równania (3.1). W przeciwnym razie realizacja algorytmu jest kontynuowana w następnym kroku.

Niech X(t) oznacza przybliżenie otrzymane w kroku k algorytmu.