skanuj0099

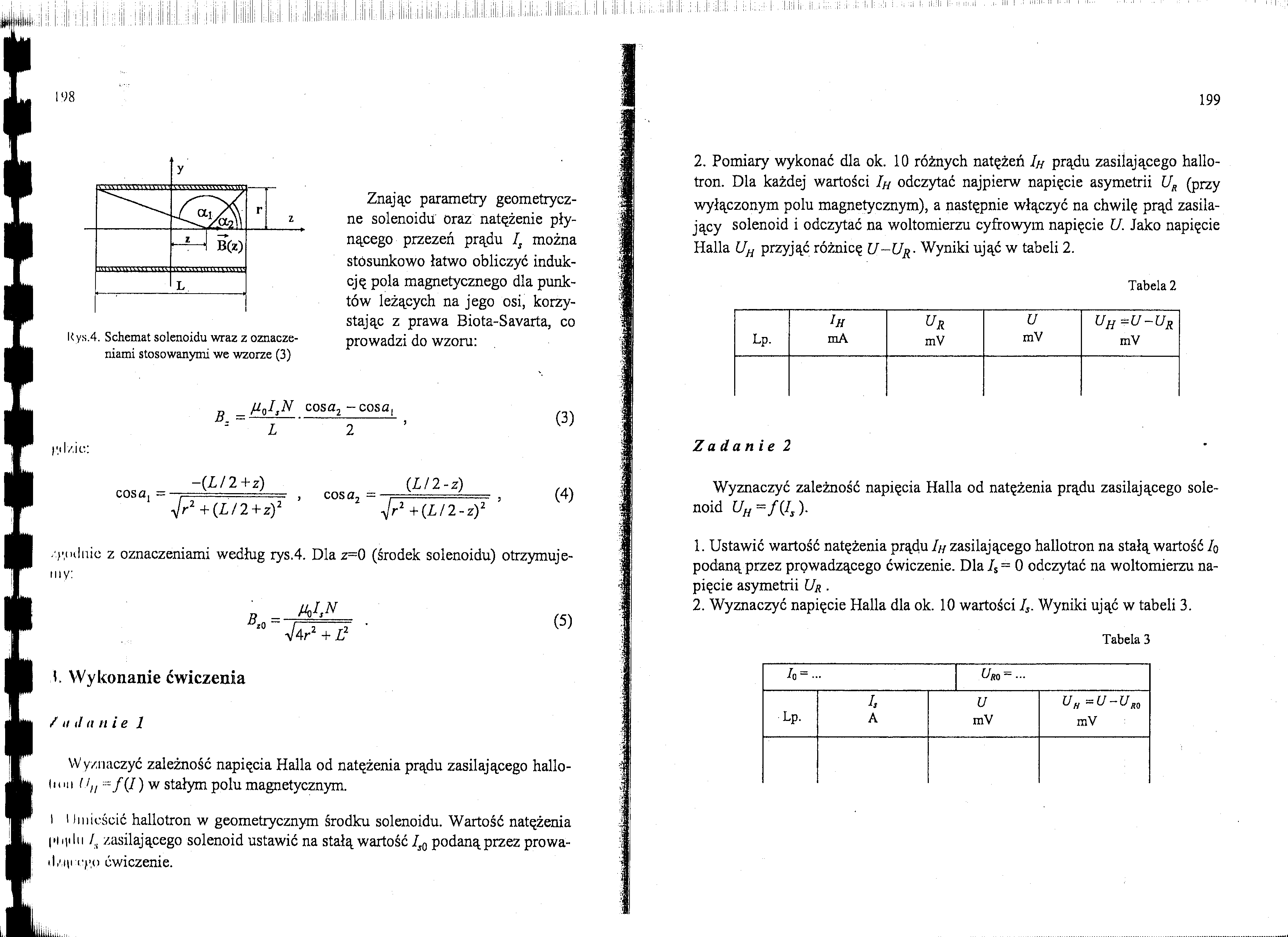
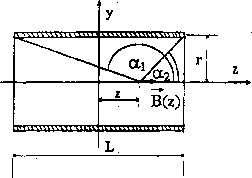
K ys.4. Schemat solenoidu wraz z oznaczeniami stosowanymi we wzorze (3)

Znając parametry geometryczne solenoidu oraz natężenie płynącego przezeń prądu I_s można stosunkowo łatwo obliczyć indukcję pola magnetycznego dla punktów leżących na jego osi, korzystając z prawa Biota-Savarta, co prowadzi do wzoru:

_ HqI₃N cosa₂ - cosa.

(3)

-{LI 2+z)

{LI 2-z)

*J    r- ............ .    ■ ....... |    WOlłi — i    '    - ■ -..... j

Jr²+{LI2+z)²    JS+{L/2-z)²

(4)

/W ulnic z oznaczeniami według iys.4. Dla z=0 (środek solenoidu) otrzymuje

my:

¹⁰ V4r² + Z,²

(5)

3. Wykonanie ćwiczenia

/ u il a n ie 1

Wyznaczyć zależność napięcia Halla od natężenia prądu zasilającego hallo-liuii U„ -f{I) w stałym polu magnetycznym.

I i (mieścić hallotron w geometrycznym środku solenoidu. Wartość natężenia pi i|i In I.₍ zasilającego solenoid ustawić na stałą wartość /_j0 podaną przez prowa-łl.-iii ••>’.<> ćwiczenie.

2. Pomiary wykonać dla ok. 10 różnych natężeń Ih prądu zasilającego hallo-tron. Dla każdej wartości I_H odczytać najpierw napięcie asymetrii U_R (przy wyłączonym polu magnetycznym), a następnie włączyć na chwilę prąd zasilający solenoid i odczytać na woltomierzu cyfrowym napięcie U. Jako napięcie Halla U_H przyjąć różnicę U-Ur- Wyniki ująć w tabeli 2.

Tabela 2

Lp.	Ih mA	Ur mV	U mV	uH^u~uR mV

Zadanie 2

Wyznaczyć zależność napięcia Halla od natężenia prądu zasilającego solenoid C/_w =/(/,).

1.    Ustawić wartość natężenia prądu Ih zasilającego hallotron na stałą wartość /o podaną przez prowadzącego ćwiczenie. Dla I_s = 0 odczytać na woltomierzu napięcie asymetrii Ur .

2.    Wyznaczyć napięcie Halla dla ok. 10 wartości I_s. Wyniki ująć w tabeli 3.

Tabela 3

7o = ...			Ur o -...
Lp.	1, A	U mV		Ur - U-Um mV