img476 (2)

Jest tylko jeden punkt krytyczny. 2) Mamy dalej

/(-1) =-2,

lim f(x) = lim

^v '    x->(- 2) ⁺

+ 1

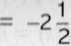
oraz

lim /(x) = lim (x + -

x->0

x—>0

= —00.

3) Ponieważ Jirn /(x) = -co, więc wartość najmniejsza tej funkcji na przedziale

(O, 2) nie istnieje, a ponieważ lim ₊/(x) < -2, więc największą wartością tej

x-*(— 2)

funkcji jest wartość y = -2 (dla x = -1). Rysunek poniżej ilustruje rozwiązanie tego zadania.

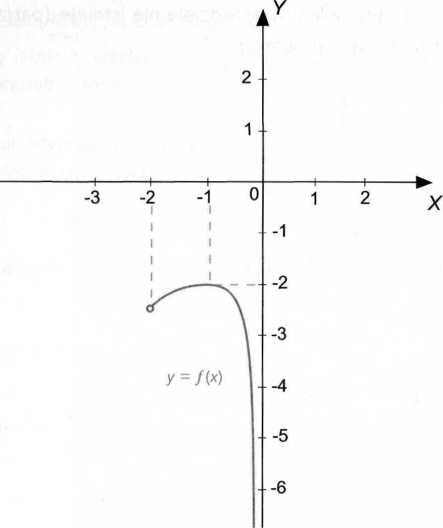
3.4. Zadania optymalizacyjne

Poszukiwanie ekstremów globalnych funkcji odgrywa istotną rolę w tzw. zadaniach optymalizacyjnych. Chodzi w nich zwykle o podanie warunków, w których koszty wykonanych operacji będą najmniejsze albo zyski największe itp. Przykłady takich zadań optymalizacyjnych podajemy na następnych stronach.

PRIYKtAD 7.

W klasie drugiej rozwiązywaliśmy (przykład 11. na str. 47. podręcznika do klasy II) zadanie o prostokątnym kąpielisku, które przylega do plaży i trzeba tak dobrać jego wymiary, aby miało jak największą powierzchnię, jeśli długość pomostu wynosi 64 m. Rozwiążemy teraz to samo zadanie, wykorzystując wiadomości o pochodnej funkcji.

y

Przypomnijmy, że oznaczając przez x długość boku kąpieliska prostopadłego do brzegu, a przez y - długość boku równoległego do brzegu, otrzymaliśmy funkcję P(x) = x(64 - 2x), przy cżym D_P - (0, 32).

Możemy teraz znaleźć największą wartość tej funkcji w tym przedziale w inny sposób. Znajdźmy najpierw punkty krytyczne.

Ponieważ

P(x) = x(64 - 2x) = -2x² + 64x,

więc

P' (x) = -4x + 64 oraz D_P = D_P.

Zatem

P'(x) = 0 o [-4x + 64 = 0 a x e (0, 32)] <=> x = 16.

Obliczamy P(16) = 512.

Ponieważ lina P(x) = lim P(x) = 0, więc funkcja P osiąga w przedziale (0, 32)

x->0    x->32

wartość największą 512 dla x = 16.

Dla x = 16, otrzymujemy y = 32, a więc pole powierzchni kąpieliska będzie największe, jeśli jego wymiary będą wynosić 1 6 m na 32 m.

PRZYKIAD8.

Dwie drogi przecinają się pod kątem prostym w punkcie P (rysunek na str. 1 24).