MATEMATYKA022

36

3. Podstawowe wiadomości o funkcjach

37

I. Wiadomości wstępne

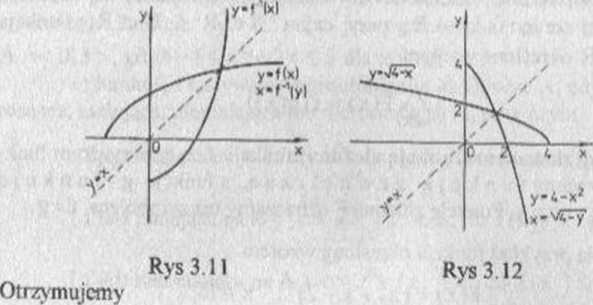
(2)    X = ^4 - y , y<=( -oo,4 >

f(x) =

(z uwagi na założenie, że x«0,+x), z dwóch możliwych znaków wybraliśmy " + "). Jeżeli argument funkcji (2) oznaczymy tradycyjnie literą x, a wartości funkcji - literą y, otrzymujemy

(3)    y = V4-x, x€(-oo,4>.

Wykresy funkcji określonych wzorami (1) i (2) są identyczne. Zauważyć jedynie warto, że argumenty funkcji (2) są punktami osi Oy, a wartości tej funkcji odkładane są na osi Ox. Wykres funkcji (3) jest symetryczny do wykresu funkcji (1) względem prostej y = x (ry s 3.12).

Warto na koniec podkreślić, że wzory (2) i (3) określają tę samą funkcję, gdyż opisują one ten sam sposób przyporządkowania dowolnemu argumentowi z przedziału (- oo,4 > odpowiadającej mu wartości funkcji.

Wzór s = V4-~t, t e (-oo, 4 > określa również tę samą funkcję ■

FUNKCJE ELEMENTARNE. Weźmy pod uwagę funkcje: stałą y * c, c€ R, tożsamościową y = x, wykładniczą y = a*, O < a * 1, i trygonometryczną y = sin x. Każdą funkcję, którą można otrzymać z wy żej wymienionych funkcji przez dokonanie na nich skończonej liczby operacji dodawania, mnożenia, dzielenia, odwracania i składania, nazywamy fbnkcją elementarną Inne funkcje nazywamy nieelementarnymi.

Na przykład każdą funkcję wymierną można otrzymać z funkcji stałej i tożsamościowej stosując dodawanie, mnożenie i dzielenie funkcję niewymierną y = y/x i funkcję logarytmiczną otrzymujemy jako funkcje • •dwtoinę do funkcji potęgowej i wykładniczej.

Przykładem funkcji nieelementamej jest funkcja Dirichlcta \ x eW,

O, x eR-W, i także funkcja określona wzorami

e\ x £0,

f(x) = ^X“l, 0<x<l, In x , x £ 1.

W dalszym ciągu omówimy, w bardzo dużym skrócie, najważniejsze z uwagi na nasze dalsze rozważania, własności pewnych funkcji lemcntamych.

WIELOMIANY. Wielomian n-tego stopnia jest to funkcja • kreślona dła dowolnego x € R za pomocą wzoru:

W(x) = a^"+a,xⁿ~'+...+a_n, a₀*0.

Wiadomo, że wielomian n-tego stopnia ma co najwyżej n pierwiastków' (i/oczywistych). Wielomian parzystego stopnia może nic mieć ani jednego pierwiastka w dziedzinie rzeczywistej, ale każdy wielomian nieparzystego ■lopnia nia co najmniej jeden pierwiastek.

Każdy wielomian może być przedstawiony jako iloczyn \\ spólczynnika a₀ oraz pewnej liczby czynników postaci (x - a), gdzie a oznacza pierwiastek tego wielomianu, i pewnej liczby czynników postaci (x^l + px + q) o wy różniku A = p - 4q < 0.

W szczególności, gdy wielomian W(x) ma n pierwiastków xx_ft (niekoniecznie różnych, gdyż uwzględniamy tu krotność pierwiastków), to

W(x) = a„(x-x,>...(x-x„).

Na przykład:

x’ +x⁴-2x’-x^j-x + 2 = (x-I)^!(x + 2)(x^j+x + 1),

2x⁵-x*+2x¹-x^j =2x^!(x-^-)(1 + x^!).