MATEMATYKA086

164 III Rachunek różniczkowy

max. lok dla x»l, min lok. dlu x«e², m) malejąca na przed/.. (-»,()), rosnące na przed/. (0,+oo). min. lok dla x=0, n) rosnąca na przędz (-2,+ao), ckstr. lok nic ma. o) malejącą na przed/ (-oo.l), (5/3,-łoo), rosnąca na przędz (1,5/3). max. lok.dla x»5/5, min.lok dla x«*l, p) rosnąca na przędz (!,+<»), ckalr. lok niema, 7.    a) Wsk. Wykazać, Ze f(x)»lnx-x<0 dla x>0; h),c) por wsk. do a).

8    a) Mox lok dla x»n/2, min lok dln x«Jt/6 i x«5xc/6, b) mux. lok dla

xe2x/3% ^m'ⁿ l°k 4la x-arccosl/3, c) max lok dln x--l, x«l, min lok. dla x*=0.

9. a) Najmniejsza wartość funkcji jeal równa y(-l)--l2, a największa: y(2)«l8;

b)    funkcja osiąga swoją najmniejszą wartość w punkcie x— 2, przy c/ym y(-2)-4c², a największą wartość w punkcie x»-l, przy czym y(-|)*c⁴; c) największa wartość funkcji: y(0)*Jc/4, najmniejsza wartość funkcji: y(2)«0;

4) y'(x)>=3sin²x(smx-cosx) = 0, gdy x = ic lub x-x/4 lub x = 5x/4 Ponieważ. y(0) = -2, y(x/4)—3/1/2, y(*)=2, y(5ic/4) = W2 , y(2x) = 2 . więc najmniejsza wartość funkcji jest równa -3/^2, a największa wartość jest rów-na 3/J2 ,

c)    najmniejsza wartość funkcji jest równa y(e²) = -2. a największa - y(c³)=2

6. WYPUKŁOŚĆ, WKLĘSŁOŚĆ, PUNKTY PRZEGIĘCIA KRZYWEJ

Wypukłość i wklęsłość krzywej Załóżmy, żc fun-

keja f jest różniczkowana na pewnym otoczeniu punktu x₀. Niech /„ będzie styczną do wykresu funkcji f poprowadzoną w punkcie P₀(x₀,f(x_o)).

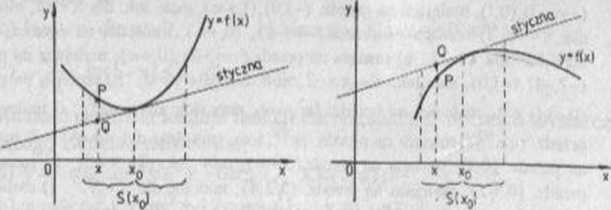
Krzywa wypukła    Krzy wa wklęsła

Rys6 l    Rys 6.2

Krzywą y = f(x) nazywać będziemy wypukłą (wklęsłą) w punkcie Xq. gdy istnieje takie sąsiedztwo S(x₀) punktu x₀, że dla każdego x eS(x₀) punkty tej krzywej leżą powyżej (poniżej) stycznej l₀ (r>'S 6.1 i 6.2).

Uściślijmy te określenia podając analityczne warunki wypukłości i wklęsłości krzywej:

Krzywa jest wypukła w punkcie x₀, gdy rzędne punktów P i Q (rys 6.1) spełniają warunek y_P>y_yt a krzywa jest wklęsła (rys. 6.2), gdy y_p <y_Q. Punkt P leży na krzywej y = f(x), więc y_p = f(x), a punkt Q lcź>' na stycznej l_ot więc y_Q = f(x₀) + f'(x₀)(x-x₀).

Zatem, przy założeniu, żc funkcja f jest różmczkowalna w punkcie x₀, przyjmujemy następujące określenia:

Krzywą y = f(x) nazywamy wypukłą w punkcie x₀, gdy f(x)>f(x₀) + f^,(x₀)(x-x₀) dla każdego x z pewnego sąsiedztwu punktu x₀.

Krzywą y = f(x) nazywamy wklęsłą w punkcie x₀, gdy f(x)<f(x₀) + r(x₀)(x-x₀) dla każdego x z pewnego sąsiedztwa punktu x₀.

Krzywą y = f(x) nazywamy wypukłą (wklęsłą) na przedziale (a.b), gdy jest wypukła (wklęsła) w każdym punkcie tego przedziału (rys 6.3).

Uwaga 1 Krzywa wypukła nazywana jest także krzywą wypukłą ku dołowi, a krzywa wklęsła - krzywą wypukłą ku górze.

U w- a g a 2. funkcję, której wykres jest wypukły (wklęsły) na pewnym przedziale nazywamy również, funkcją wypukłą (wklęsłą) na tym przedziale.

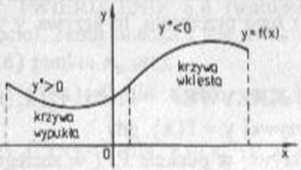
Rys 6.3

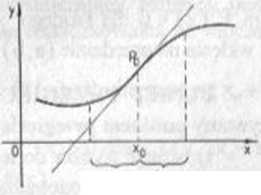
S‘l*_al S-t*c> Rys 6.4