MATEMATYKA057

106 III Rachunek różniczkowy

T wierdzenia 1,4 - 1.6 oraz analogiczne do nich. można zapisać w sposób umowny (por. rozdz 11,1) w postaci równości:

g±»-±00,    ±X±Q0=±00,

g(±oo) -±cc dla g>0, g(±oc) -    dla g<0,

(±00)(±=C) = + «>, _g_    J_    J_

(ioo)(Toój* •», ±x    ’0+    0-

Powyższe twierdzenia nic pozwalają nam stwierdzić, jaka jest granica różnicy (f (x) - g( x)). gdy

limf(x) = +a>    i limg(x) = -too

x-*x„    x

Mówimy wtedy, żc różnica (f(x)-g(x)) jest w punkcie x„ wyrażeniem nieoznaczonym (symbolem nieoznaczonym) typu cc-oc. Analogicznie: iloczyn f(x)g(x) jest w punkcie x₀ wyrażeniem nieoznaczonym (symbolem nieoznaczonym) typu 0-x, gdy

limf(x) = 0 i limg(x) = +oc.

X-K\„    X-»X„

Niżej podajemy wszystkie symbole nieoznaczone:

CC - 00

0- CC,

00

00

o

0’

0°,

oo

W przypadku symboli nieoznaczonych bezpośrednie stosowanie wcześniej poznanych twierdzeń o granicach jest niemożliwe W celu obliczenia granicy funkcji należy wtedy, stosując odpowiednio dobrane do funkcji i rodzaju symbolu nieoznaczonego przekształcenie, zapisać funkcję w takiej postaci, by twierdzenia te mogły być zastosowane

PRZYKŁADY OBLICZANIA GRANIC FUNKCJI

PRZYKŁAD 1.5 Obliczvnw granice: 3    1

lim ^x V x

a) lim    —|

x~* «• 2x‘ + 5 1 I

b) lim (x-x²>/x^ł-5)= lim x(l -\-J\^% -5) = {(+oc)(-»)} = -x;

5~x \-ooj _Xłfoo 5    \ -1 J ⁰⁰¹

_x .. 2x³+Vx

c) lim-_r

X H» 5-

A

d) lim (y-=    i»_n (^“/^x2~¹)(^x ł-Vx²-l)

^x“~"    — xWx²-l

lim-J......

^{x M}"x+Vx²-I

c) lim (x-Vx²-l) = { -oc-oc } = -oo;

X->-eO    ^J

1 -X²

O lim 2arcsin-—₇ = 2arcsin(-l) = -7i;

*•+-* l + x‘

*>

B> £”V(^XŁ2arclg-^) = {i oo-2arclg(4-x)} = {+«-_x} = +oo;

2-3 * + l

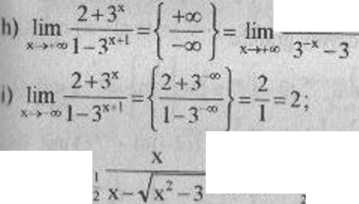
j) lim log

k) lim (~²)^h'={ |" }    lim((l+-L)*^,*)4=c^,!;

*-*+» X*    ^J X»'«    x^2/2

3 ’

.. .    x(x+Vx²- 3) |    I

= hmtog.-i— -Mlc*,(-ko) - -®;

$mx

¹¹ ^oT* ⁼ ° ^na P^odatawic iwierd/cnia o granicy Irzech funkcji, gdyż

I . sin x I „    i    i

~x^ś~x~~x' ^{x>0 oraz    lim}(—)= lim — = 0.

^{X X x}    *- M*0 X X »»»X