59980 MATEMATYKA093

178 III. Rachunek różniczkowy

Wnioskujemy także o istnieniu ekstremów lokalnych - maksimum w punkcie x = 2 i minimum w punkcie x = 6.

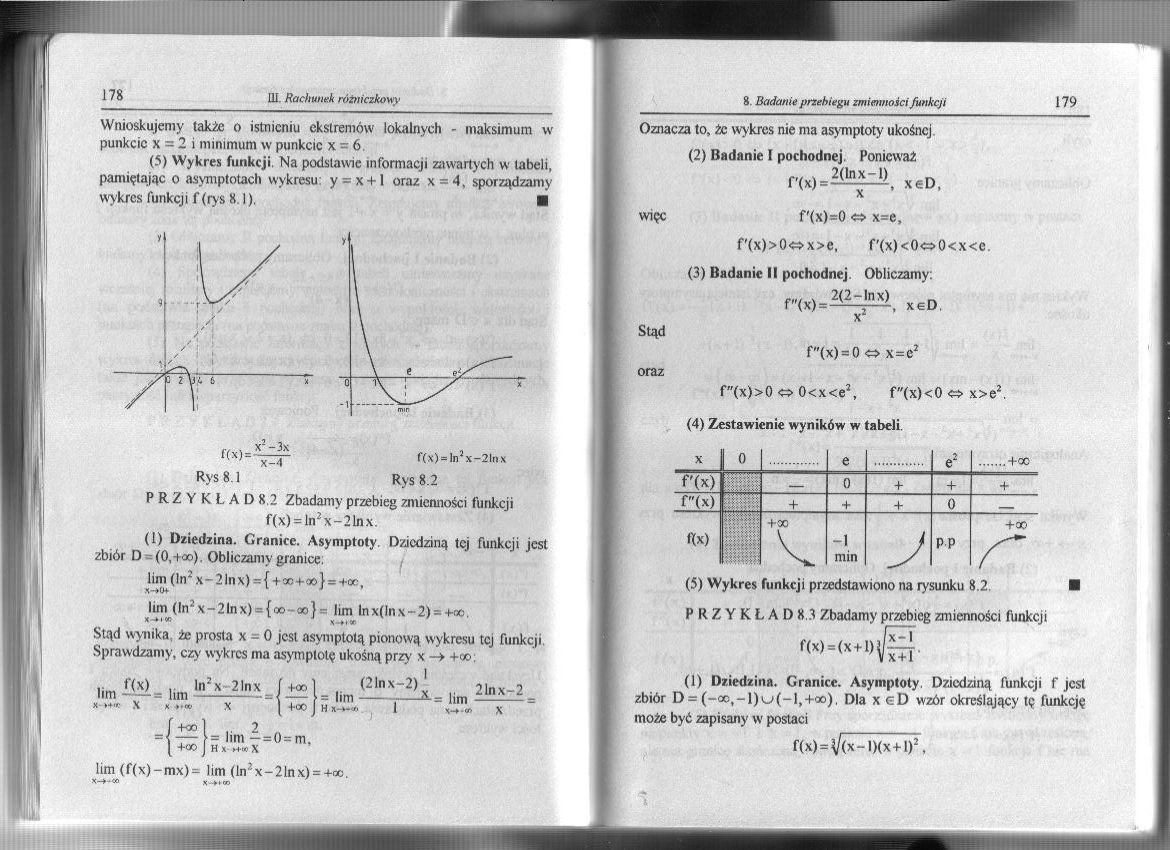
(5) Wykres funkcji. Na podstawie informacji zawartych w tabeli, pamiętając o asymptotach wykresu: y = x + 1 oraz x = 4, sporządzamy wykres funkcji f (rys 8.1).    ■

Rys 8.1    Rys 8.2

PRZYKŁAD 8.2 Zbadamy przebieg zmienności funkcji f(x) = ln²x-21nx.

(I) Dziedzina. Granice. Asymptoty Dziedziną tej funkcji jest zbiór D = (0,+oo). Obliczamy granice.    /

lim (ln² x-2lnx) = { + x+<*>} = -for, x-*Of

lim (ln‘x-2lnx) = {oo-oo}= lim lnx(ln.\-2) =-ł-cc.

x~*i«    X-*««

Stąd wynika że prosta x = 0 jest asymptotą pionową wykresu tej funkcji. Sprawdzamy, czy wykres ma asym plotę ukośną przy x —> +co;

,_jmfW^_lim!nV2lnx

x X x ►    X

+O0

+00

<^2lnx-²)_x    ..    21nx-2

= lim-:-*-= lim-

H X-*-*¹    I    x-*.«    X

= (—1= lim —=0= m.

( +00 J H x ►+* X

lim (f(x)-mx)= lim (ln² x-2lnx) = +<*>•

Oznacza to, że wykres nie ma asymptoty ukośnej. (2) Badanie I pochodnej. Ponieważ

_ft/ . 2(lnx-l) ~ f(x) = ---_x    . xeD.

więc

Stąd

f'(x)=0 o x=e,

f'(x)>0<=>x>e,    f'(x)<0o0<x<e.

(3) Badanie II pochodnej. Obliczamy:

r(x_)a²⁽²-'ⁿ*>, x€D.

X“

f"(x) = 0o x=c² oraz

f”(x)>0    0<x<e²,    f"(x)<0 <=> x>e².

(4) Zestawienie wyników w tabeli.

X	0		e		e*	.....+x
f'(x)		_	0	+	+	+
f"(x)		+	+	+	0
flx)		+x	-1 min	J	pp	+00

(5) Wykres funkcji przedstawiono na rysunku 8.2.    ■

PRZYKŁAD 8.3 Zbadamy przebieg zmienności funkcji

^f(x>“<*^+l>&

(1) Dziedzina. Granice. Asymptoty. Dziedziną funkcji f jest zbiór D = (-oc,-l)w(-l,+oo). Dla x gD wzór określający tę funkcję może być zapisany w postaci

r(x)=V(*-»(x+i)².