MATEMATYKA089

170 HI. Rachunek różniczkowy

7. ASYMPTOTY KRZYWEJ

ASYMPTOTY PIONOWE Załóżmy, żc funkcja f jest określona na pewnym sąsiedztwie punktu a.

Prosta x = a nazywamy asymptotą pionową krzywej y = f(x), gdy przynajmniej jedna z granic jednostronnych funkcji f w punkcie a jest niewłaściwa tzn.:

limf(x) = ±co lub limf(x) = ±oo.

X—X-**f

W przypadku gdy tylko jedna z tych granic jest niewłaściwa, mówimy o asymplocie pionowej jednostronnej - lewostronnej lub prawostronnej. Jeżeli obie te granice są niewłaściwe, mówimy, że prosta x = a jest asymptotą obustronną.

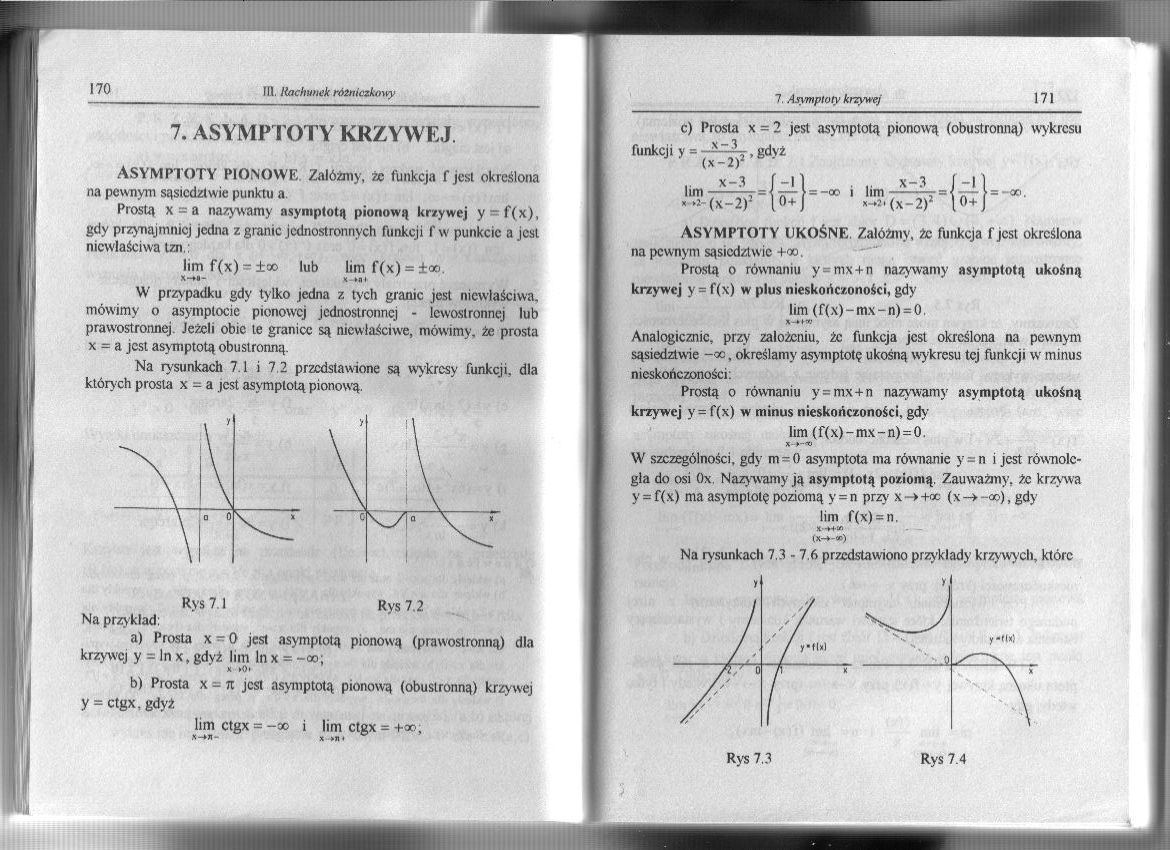
Na rysunkach 7.1 i 7 2 przedstawione są wykresy funkcji, dla który ch prosta x = a jest asymptotą pionową.

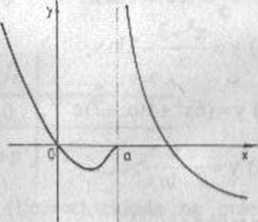
Rys 7.1 Rys 7.2

Na przy kład:

a) Prosta x = 0 jest asymptotą pionową (prawostronną) dla krzywej y = In x, gdvż lim In x = -oo;

X ►<)•

b) Prosta x - n jest asymptotą pionową (obustronną) krzywej y = ctgx. gdyż

lim ctgx = -x i limctgx = +oo,

X-*X- X **«

ASYMPTOTY UKOŚNE. Załóżmy, źe funkcja f jest określona na pewnym sąsiedztwie +oo.

Prostą o równaniu y=mx + n nazywamy asymptotą ukośną krzywej y = f(x) w plus nieskończoności, gdy

lim (f(x)-mx-n) = 0.

Analogicznie, prz>' założeniu, że funkcja jest określona na pewnym sąsiedztwie -oc, określamy asymptotę ukośną wykresu tej funkcji w minus nieskończoności:

Prostą o równaniu y = mx + n nazywamy asymptotą ukośną krzywej y= f(x) w minus nieskończoności, gdy

lim (f(x)-mx-n)=0.

W szczególności, gdy m = 0 asymptota ma równanie y = n i jest równoległa do osi ()x. Nazywamy ją asymptotą poziomą. Zauważmy, że krzywa y = f(x) ma asymptotę poziomą y = n przy' x -» -kc (x -> -co), gdy

lim f(x) = n.

Na rysunkach 7.3 - 7.6 przedstawiono przykłady krzywych, które

. -

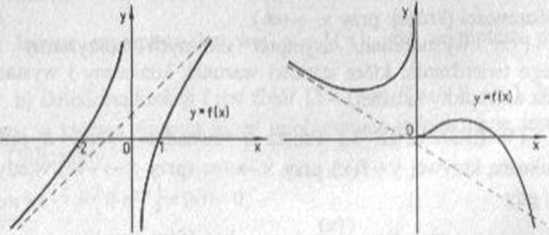
Rys 7.3

Rys 7.4