MATEMATYKA061

114 HI Rachunek różniczkowy

2. CIĄGŁOŚĆ FUNKCJI

FUNKCJA CIĄGŁA. Funkcję f, określoną na pewnym Otoczeniu punklu x₀, nazywamy ciągłą w punkcie x₀, gdy ma w tym punkcie granicę równą swojej wartości, czyli

lim f(x)=f(x₀).

*-*x₀

Jeżeli funkcja f. określona na pewnym otoczeniu punktu x₀, nic jest w tym punkcie ciągła, to x₀ nazywamy punktem nieciągłości funkcji f.

Punkty nieciągłości, w których funkcja ma obie granice jednostronne skończone nazywamy punktami nieciągłości pierwszego rodzaju, a pozostałe punkty nieciągłości - punktami nieciągłości drugiego rodzaju.

Z twierdzeń o granicach funkcji i przyjętej definicji funkcji ciągłej wynika, że

(1)    Suma, różnica i iloczyn funkcji ciągłych w pewnym punkcie jest funkcją ciągłą w tym punkcie.

(2)    Iloraz funkcji ciągłych w pewnym punkcie jest funkcją ciągłą, przy założeniu, że jest określony w tym punkcie.

(3)    Jeżeli finkcja złożona F(x) = f(g(x)) jest określona na pewnym otoczeniu punktu x₀, przy czym funkcja g jest ciągła w punkcie x₀. a funkcja f jest ciągła w punkcie U₀ = g(x₀), to funkcja F jest funkcją ciągłą w punkcie x₀.

Funkcję f nazywamy ciągłą lewostronnie w punkcie x₀, gdy jest ona określona w punkcie x₀ i na pewnym lewostronnym sąsiedztwie tego punktu oraz

lim f(x) = f(x„).

M-M₀-

Fupkcję f nazywamy ciągłą prawostronnie w punkcie x„ , gdy

jest ona określona w punkcie x₀ i na pewnym prawostronnym sąsiedztwie tego punktu oraz

lim f(x) = f(x„).

K-*X₀ +

Funkcję f nazywamy ciągłą na przedziale otwartym (a,b), gdy jest ciągła w każdym punkcie tego przedziału. Funkcję nazyw-amy ciągłą na przedziale domkniętym <a,b>, gdy jest ciągła w każdym punkcie wcwnętrzym tego przedziału oraz prawostronnie ciągła w punkcie a i lewostronnie ciągła w punkcie b.

Wykazuje się, 2c:

Każda funkcja elementarna jest funkcją ciągłą w dowolnym punkcie swojej dziedziny.

Zatem funkcje y = 3-x\ y = sin2x, y = x2^{x l}, y = cos’3x są funkcjami ciągłymi na zbiorze R. Funkcja y = ln(2 + x) jest funkcją ciągłą

\

w dowolnym punkcie xe(-2,+oo), a funkcja >' ⁼ y^ jest ciągła w

każdym punkcie x*-3.

Natomiast funkcja

-2-x	dla	X €(-QO,-l),
X+1 1 X	dla	x €<-L,0>,
	dla	X€(0,+Oo)

(por. rys 2.1), określona dla każdego x € R, jest funkcją ciągłą w każdym punkcie dziedziny z wyjątkiem punktów' x, = -1 oraz x₂ = 0.

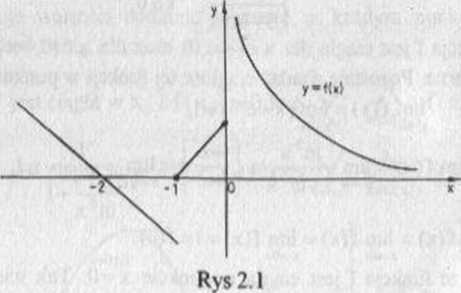
Ponieważ lim f(x) = -l, lim f(x) = 0 (granice jednostronne są

»-» I    X ► |4

różne, ale skończone), więc x, = -1 jest punktem nieciągłości pierwszego rodzaju Natomiast punkt x₂ = 0 jest punktem nieciągłości drugiego rodzaju, gdyż limf(x) = l, limf(x) = +oo.

x-»0    x *0.