MATEMATYKA075

142 HI. Rachunek różniczkowy

Uwaga I. Twierdzenia odwrotne do wniosków DI i IV nie su prawdziwe Na przykład funkcja f(x)»x^ł jest rosnąca na zbiorze R, a jej pochodna f'(x)«3x² jest równa zera dla x»0.

Prawdziwe jest twierdzenie

ieteli funkcja f jest różniczkowa Ina i rosnąca (malejąca) na przedziale (a.b). to f'(x) £ 0 (f'(x) <, 0) dla każdego x e(a,b).

U w a g a 2. Wnioski I - IV przestają być prawdziwe, gdy zastąpimy w nich przedział (a,b) dowolnym zbiorem (np sumą przedziałów rozłącznych) Na przykład:

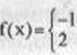
dla xc(-2,-l), dla x €(—1,1),

a) funkcja

ma pochodną równą zeru w każdym punkcie zbioru A*(-2,-l)u(-l,l), ale nic jest funkcją stałą nu tym zbiorze.

b) Funkcja f(x)=ctgx ma ujemną pochodną w każdym punkcie dziedziny D={xeR: x*kJt,keC}, ale funkcja ctg nic jest funkcją malejącą w całej swojej dziedzinie (jest funkcją przedziałami malejącą).

PRZYKŁAD 4.1 Wyznaczymy przedziały monotoniczności

Funkcji    f(x)»c^(3x>\

Funkcja f jest określona dla xeD = (-oo,3)u(3,+oc) i jest różniczkowalna w⁽ każdym punkcie zbioru D, przy czym

i

f'(x) =

3

(3-x)⁴

Widać, źc f'(x)>0 dla każdego xeD. Zatem (wniosek III) funkcja f jest rosnąca na przedziałach (-oo,3) oraz (3,+ao).    ■

PRZYKŁAD4.2 Wymaczymy przedziały monotoniczności

„ .    *•/ v x*-3x + 4

funkcji    f(x) = —^—

Funkcja la jest określona dla x e D = (-oo,3)u(3,+oo) i w tym też zbiorze jest rożniczkowalna, przy czym

x²-6x-ł-S '    (x-3)² •

Stąd wynika, źc dla x e D

y	|y *<0 „
	\ J* .»? -fa+Ł. \ ^1 *"^3 1 i'
	1 /
	A •
0	^1 !
✓	J 3 \ \l
Ar
Si> c	li /<o«i

f'(x)>0 o x^:-6x + 5>0, f'(x)<0 o x²-6x + 5<0.

Ponieważ f'(x)>0 dla x<l lub x > 5, więc na przedziałach (-oo, 1) oraz (5,+«) funkcja f jest rosnąca Ponieważ f'(x)<0, gdy 1 < x < 3 lub 3 < x < 5, więc na przedziałach (1,3) oraz (3,5) funkcja f jest malejąca. Na rysunku 4,3 przedstawiony jest wykres tej funkcji.    ■    Rys 4.3

PRZYKŁAD 4.3 Wykażemy, źc funkcja określona wzorem

f(x) = aresin

7

² +1

-arctgx

jest funkcją stalą na zbiorze liczb rzeczywistych.

Ponieważ nierówność

-1<—^=<1 v x² +1

jest spełniona dla każdego x eR, więc dziedziną funkcji f jest zbiór R. Dlakażdego xeR mamy

Vx^ł+l——

1    2vx^ł + 1__L_ ₌₀

f'(x) =

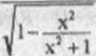
x* + l

x^ł + l

Zatem, zgodnie z wnioskiem I z twierdzenia Lagrangc’a, funkcja f jest stała na zbiorze R Obliczymy wartość tej funkcji w dowolnie wybranym punkcie np x = 0;

f(0) = aresin 0 - arctgO = 0.

Zatem f(x) = 0 dla każdego x e R.    ^    ■

PRZYKŁAD 4 4 Wykażemy, że

_rx—1 f-3tt/4 dla x<-l, ⁵x+1( x/4 dla x>-l.

arctgx -arctg^: