MATEMATYKA146

282 V. Całko oznaczona

(3)    lim |/J= lim £7¹ + [f'(x,)l^!Ax,

n    a-**¹

(d„-*0)    (d„ »0) ^{1 1}

Z równości (1) wynika, żc d_n->0o5_n->0. Prawa strona (3) jest

granicą ciągu sum całkowych funkcji -^1 + [f'(x)]^{2 3 4}. Funkcja ta, wobec ciągłości pochodnej f', jest ciągła, a więc i całkowalna Zatem granica ta istnieje i jest całką oznaczoną tej funkcji:

n - ^h. -

(4)    lim XV^l+[^f'(⁵‘,)]^:Ax,=JV¹-^ł[^f'(x)]^Jdx

<«ł. -*0) ^i=l    •

Z równości (4. ł), (2), (3) i (4) wynika wzór (4.2).    □

PRZYKŁAD 4.1 Linią łańcuchową nazywa się krzywą określoną równaniem;

y = f(e^xa + c ^v*) = acosh—, a = const>0, xeR. z    a

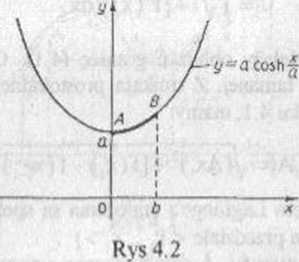
Ma ona kształt nicrozciągliwego łańcucha zawieszonego w dwóch punktadi, (por. rys 4.2),

Obliczymy długość łuku tej linii, odpowiadającego przedziałowi <0.b>, daną wzorem (4.2). Obliczamy najpierw wyrażenie 1 +[f'(x)]'’;

Zatem, zgodnie z (4 2),

|/|= J Jl(e«^/*+e-"*)^:dx = i)(e”"+e ‘*)dx = ±a(e* e «'■)[ -

o    o

= ®(e^h’-e *').    ■

Po łych szczegółowych rozważaniach dalej będziemy ograniczać się tylko do formułowania twierdzeń i rozwiązywania przykładów.

TWIERDZENIE 4.2 Jeżeli łuk I dany jest równaniami parametrycznymi

/: x = x(t), y = y(t), a<t£f)

i przy tym różnym punktom t z przedziału (a,P) odpowiadają różne punkty tego łuku (łuk nic ma punktów wielokrotnych) oraz funkcje x(t) i y(t) są klasy C na przedziale <a,(3 >, to długość |/| łuku / wyraża się wzorem:

(43)    |/i=}V[x'(t>f+[y'<t)fdt

a

PRZYKŁAD 4.2 Cykloidą nazywa się krzywą, jaką zakreśla ustalony punkt okręgu toczącego się bez poślizgu po prostej (ry s 4.3). Można wykazać, że opisują ją równania parametryczne postaci x = r(t - sin t), y = r(l - cost), gdzie r jest promieniem toczącego się okręgu, natomiast parametr t - miarą łukową kąta, o który obróci się okrąg w procesie toczenia.

Wykorzy stując wzór (4.3) obliczymy długość łuku cykloidy zakreślonego przy pełnym obrocie toczącego się okręgu, tj. dla 0 £ t £ 2ft.

y-rO-coł/)

1

₊[f'(x)]^J = 1 +bU(V* -ie    = l+[i(e"" -e =

2

— ii    n    Z

3

= ^[4 + (e"')² - 2e*^/‘e * + (e"*)^ł]«= \ [(c^v,>² +

4

+2e*^/‘tT^xt‘ +(e'^x''*)^J] = i(e^x>