MATEMATYKA147

284 V. Całko oznaczona

Ponieważ

fx'(l)]‘+fy'(t)]^: =|r(l-cost)|^:+[rsint]²=2r(l-cost)=4r²sin²(i/2),

V(x'(t)|^,+|y'(l)]’ = ^4r²sin^J(t/2) = 2r|sin(t/2)|,

więc zgodnie z (4.3), otrzymujemy:

2«    2*

|/|= J 2r|sin(t/2)|dt = 2r Jsin(t/2)dt = 4rcos(t/2)|”_ii = 8r ■

0    0

DŁUGOŚĆ ŁUKU W UKŁADZIE BIEGUNOWYM. Najpierw wprowadzimy pojęcie układu współrzędnych biegunowych.

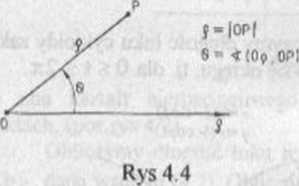
Gdy na płaszczyźnie zorientowanej obierzemy dowolny punkt O zwany biegunem oraz półproslą Op , skierowaną w prawo, zwaną osią biegunową, to powiemy, żc na płaszczyźnie został określony układ współrzędnych biegunowych (krócej: układ biegunowy), (por. rys 4.4).

Każdemu punktowi P -A O w tym układzie w^rspół rzędnych odpowiada para liczb (p,0) - współrzędnych biegunowych tego punktu. Przy tym współrzędna p jest odległością punktu P od bieguna O, zaś współrzędna 0 jest miarą łukową kąta skierowanego, jaki tworzy promień wodzący punktu P z osią biegunową ,(rys 4.4).

•c

o    p

Rys 4.5

PRZYKŁAD 4.3 Na rysunku 4.5 zastały zaznaczone punkty o zadanych współrzędnych biegunowych. A(2,*/4), B(3,k/4), D(!,jt/2), Ł(l,5a/2), F(2,te/2), G(2,3rt/4), H(2,n). Warto zwTÓcić uwagę żc: I) punkty A, B, C leżą na jednej prostej (ich druga współrzędna jest

jednakowa), 2) punki D jesi identyczny z punktem E mimo, źc nie obydwie ich współrzędne są równe, 5) punkt)' A. F, G, H należą do okręgu o środku w biegunie O i promieniu r = 2.    ■

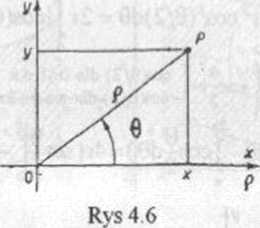
Na płaszczyźnie obierzmy, lak jak na rysunku 4 6, dwa układy współrzędnych; prostokątny Oxy i biegunowy. Dowolny punkt P ma Wtedy współrzędne (x,y) w układzie prostokątnym i współrzędne (p,0) w układzie biegunowym Łatwo wyprowadza się następujące zależności między tymi współrzędnymi

(1)    ^ = x²+y², x = />cos0, y = psin 0.

PRZYKŁAD 4.4 W prostokątnym układzie współrzędnych równanie x² + y² = r² przedstawia okrąg o środku w początku układu i promieniu r. Korzy stając z zależności (1) otrzymamy równanie p= r tego okręgu w układzie biegunowym;

x² + y^: = r o(pcos0 )² + (/?sin0 )² = r o/T = r² op= r. ■

TWIERDZENIE 4.3 Jeżeli łuk / dany jest w układzie biegunowym równaniem

p=f(Q), aśOśp, p-a£27t, gdzie f jest nicujemną funkcją klasy C na przedziale <a,p>, to jego długość |/j wyraża się W'zorcm

(4.4)    |/|=}Vf^J(0)₊[f(e)f^!de

a

PRZYKŁAD 4.5 Obliczymy długość luku jeszcze jednej krzywej pochodzenia mechanicznego - kardioidy, czyli krzywej sercowej