51402 MATEMATYKA131

252 V. Całka oznaczona

Ponieważ x, - x₍_, - Ax, oraz O' = f, więc

0(x,)-<l)(x₍._l) = f(x,)Ax,, i = 1,2.....n

W konsekwencji mamy

0(b)-0(a) = £f(x,)Ax,

•-i

Zauważmy, że lewa slrona ostatniej równości nic zależy od n. a jej prawa strona jest sumą całkową ciągłej, a więc i całkowalnej funkcji f na przedziale < a, b >. Niech n -» a> i jednocześnie 5_ -» 0. Wówczas

Ponieważ

lim (<D(b)-0>(a))= lim Yf(x)Ax,.

n. ki/i    u

n-»«*    n-*oo

(«.-*<») <*„ »0) '^u|

lim (0(b)-cP(a)) = <D(b)-cI)(a)

n-w>

oraz

i=i

lim Zf(x_i)Ax_i=Jf(x)dx,

<*• *o)

więc

n

0(b)-d>(a) = jf(x)dx

Uwaga. Wzór (2.1) pozostaje prawdziwy, gdy a > b, ponieważ wtedy:

b    def ^a

Jf(x)dx = -Jf(x)dx = {tw.2i}=-(<I>(a)- <J>(b))=<I>(b)-<l>(a).

Q    b

PRZYKŁAD 2.1 a) Jedną z funkcji pierwotnych funkcji f(x) = cos2x jest funkcja 0(x) = -sin 2x, dlatego

"f    .    «/«    .    «

J cos2xdx = ^sin 2x = y (sin ~ - sin 0) =

253

2. Obliczanie i własności całki oznaczonej

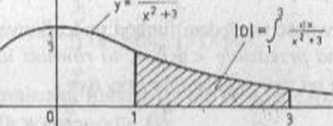
Rys 2.1

b) Pole |D| figury D (rys 2.1) ograniczonej liniami y = 0, y=(/(.W), x^l,x = 3, tj. D---{(x,y)€Rⁱ:lSxS3,0£ySl/(3+x^J)}, zgod-nic z interpretacją geometryczną całki oznaczonej, wyraża się wzorem.

Jedną z funkcji pierwotnych funkcji podcałkowej jest funkcja

X    •    •

-^aretg-y--, więc, na podstawie wzoru Ncwtona-Lcibniza, otrzymujemy

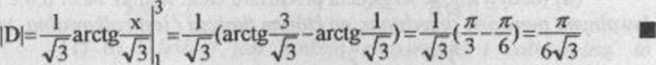
WŁASNOŚCI CAŁKI OZNACZONEJ. Niektóre własności całki oznaczonej poznaliśmy już wcześniej. Sformułujemy teraz dalsze jej własności.

(I) Wartość całki oznaczonej nie zależy od oznaczenia zmiennej całkowania:

b

b

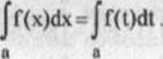
Na przykład

J^-=2^|‘=2(x/4-/i)=2 i J-^ = 2Vt[-2(V4-VT)-2.