Matem Finansowa"6

226 Zbiór zadań i testów z matematycznych podstaw teorii procentu

51)    Dla funkcji intensywności oprocentowania kapitału 5t = 0,05 t wyznaczyć równoważne jej w okresie 3 lat stopy dyskontowe i procentowe:

a) d    b) d⁽⁴⁾    c) i    d) i⁽²⁾

52)    Obliczyć zgodnie z regułą bankową czas w latach między datami 14 lutego 1999r. a 15 kwietnia 1999r.

53)    Obliczyć liczbę dni między datami: 3 maja 1999r. i 11 listopada 1999r:

a) w sposób dokładny    b) w sposób przybliżony

54)    Obliczyć procent prosty od 1000 zł dla rocznej stopy procentowej i=24% za okres od 3 maja 1999r. do 11 listopada 1999r. Obliczenia przeprowadzić z uwzględnieniem różnych sposobów liczenia czasu:

a) procent dokładny    b) procent bankowy (reguła przybliżona)

c) procent zwykły    d) procent przybliżony (reguła przybliżona)

55)    Zbadać czy następujące funkcje są funkcjami dyskontowania jednostki kapitału?

^a)d'W=ITT ^b)d>^w=(!^feT3j ^c)d3(t)=r‘ d)d₄(t)=2-²

56) Dla funkcji dyskontowania jednostki kapitału z zadania 55. wyznaczyć: a) odpowiadającą funkcję oprocentowania jednostki kapitału

b)    efektywną stopę procentową i_n

c)    efektywną stopę dyskontową d_n

d)    dyskonto za n okresów wstecz Dⁿ

e)    funkcję intensywności dyskontowania kapitału 6,.

57) Funkcja intensywności dyskontowania kapitału ma postać: 5'_t =ln(l+t). Wyznaczyć funkcję dyskontowania jednostki kapitału (czynnik dyskontujący).

58) Wyznaczyć stałą roczną intensywność dyskontowania, która w ciągu 30 lat jest równoważna zmiennej intensywności dyskontowania

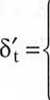
0,05

0,06

0,07

dla te<0,5> dlate(5,20> . dla te (20,30>