new 91 (2)

186

7. Zasady obliczeń wytrzymałościowych śrub

gdzie:

p,„ =

nQ_w

ab

P*_

ab

Pm_x

M_x

Pm

My,

yz

a² b    ab‘

~6~    1T

a maksymalne naciski w punkcie A nie powinny przekraczać nacisków dopuszczalnych

Pmax ' Pu Pz P^Mxz P^yz ^ P^d0P*    (7.167)

Składowe obciążenia roboczego śrub wynikające z siły P_z oraz momentów'

M_xz i M_v, są odpowiednio równe

Qr —

Qr =

Pz_ n ’

M l

^!,ir*^lrraa)t

2

... M l

_ -^irłyz^Łi/TrvaJC

r —

2 Sl*

tri

(7.168)

(7.169)

(7.170)

gdzie jest odległością od osi śrub do środka ciężkości styku mierzoną wzdłuż osi x; l_ul — odległością od osi śrub do środka ciężkości styku mierzoną w^rzdłuż osi y (dla przykładu przedstawionego na rys. 7.54

Myz

wszystkie odległości l_vl) l_vmix są równe, stąd Q_r^: n jest liczbą śrub).

2 nl

y max

, przy czym

Całkowite obciążenie najbardziej obciążonej śruby jest równe

M„J_U

Qc = Q„ +

f

przy czym C_x i C₂ oznaczają sztywność śruby i sztywność elementów łączonych.

Przytoczony schemat obliczeń dotyczy układu, w którym środki ciężkości powierzchni styku i przekroju wszystkich śrub pokrywają się. W przeciwnym przypadku do obliczeń należy wprowadzić korektę, a mianowicie do wzorów (7.166) i (7.167) należy podstawić nacisk p_w wyrażony wzorem (7.138) oraz nieco inaczej zapisać wzór na całkowite obciążenie najbardziej obciążonej śruby:

Qw "1“

M„

Pz

n

M_x,—Pe_x

22(1*-e,)*¹’

e*) +

(7.172)

- (I

-o \'^ ^v

-c»)

C,

c,+c.

m»-eyV

Zasady obliczeń wytrzymałościowych śrub są takie jak w punkcie 7.5.6.

7.7. Przykłady obliczeniowe

187

Obciążenie P_x, P_y i M_xy działające w płaszczyźnie styku przenoszone są przez tarcie przy styku płaskim lub przez powierzchnie oporowe przy kształtowym sprzężeniu elementów łączonych (patrz rys. 7.53g, h).

Aby nie nastąpiło przemieszczenie względne elementów łączonych przy styku płaskim powinny być spełnione następujące warunki

I

T = fi{Q_wn—P_:) > \ Pl f Py , M_t = /up o dF_s = fipS₀ > M_xv,

(7.173)

(7.174)

Q Yl _ p,

gdzie p = -    ^ ^r jest średnim naciskiem na powierzchnie styku,

aS„ = \ q dF_s — biegunowym momentem statycznym powierzchni styku względem środka ciężkości styku.

7.7. Przykłady obliczeniowe

Przykład 7.1. Obliczyć wymiary nakrętki dwustronnej, jeśli siła działająca na ściąg jest równa Q — 20 kN. Materiał ściągów i nakrętki stal St4 o granicy plastyczności R_e = 250 MPa.

Wartość dopuszczalnych naprężeń na rozciąganie (ściągów) przy założeniu współczynnika bezpieczeństwa X_c=l,7 wynosi

, R_e 250    ._

k_r = —Ł- =    = 147 MPa.

Ae    l»«

Średnicę wewnętrzną gwintu śruby obliczamy wstępnie ze wzoru (7.28)

r

d₃ = 1,27 j/

Q

kr

= 1,27

l~ 20000

|    147

= 14,81 mm.

Przyjmujemy gwint M18 o d₃ = 14,712 mm i sprawdzamy według wzoru (7.22). W tym celu obliczamy w ściągu naprężenia rozciągające

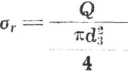
4-20000 it* 14,712®

- =117,6 MPa

i naprężenia skręcające

M_s 0,5Qd,tg(y+e')    0,5-20000-16,356-tg 9,372°

^T’ W₀    -dl    ~    x-l4,712^ł

16

= 48,3 MPa,

16