PA300003

może zatem nastąpić tylko wówczas, gdy do końca A liny przyłożymy siłę P równą co do wartości liczbowej sile Q. A zatem

P=Q.

W linie przerzuconej przez krążek 5 i obciążonej siłą Q napięcie (przy pominięciu oporów tarcia na osi krążka) jest jednakowe na całej długości liny i równe Q.

Wartość siły S, będącej siłą oddziaływania liny BD na krążek B, będzie równa wartości wypadkowej R sił P i Q, a jej linia działania będzie dwusieczną kąta a. Zatem w linie BD powstanie siła S = R, a sama lina odchyli się od pionu o kąt /? = = */2 (rys. c).

Wartość wypadkowej R (a więc i »Sj wyznaczymy z zależności

R    R P    P

skąd

1.14.

sin(180°—a)    sina    sin/?    sin(a/2) *

S=P =    = 2Pcos(«/2).

sm(a/2)    ^v ' ⁷

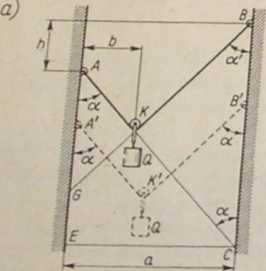
/ W punktach A i B położonych na różnych wysokościach dwóch piono-I wych ścian znajdujących się w odległości a jedna od drugiej, zamocowano końce liny, której długość wynosi l. Po linie tej może się poruszać — z po-mijalnie małymi oporami tarcia — lekki krążek K z zawieszonym ciałem o ciężarze O. Znaleźć siłę napięcia liny S oraz położenie krążka odpowiadające stanowi równowagi, wiedząc, że różnica wysokości punktów zaczepienia A i B łiny wynosi h.

b)

1

Rys. do zad. 1.14

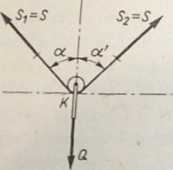
Rozwiązanie. Przyjmijmy, że krążek K z ciężarem O, mogący poruszać ę po linie z pomijalnie małymi oporami* tarcia, w położeniu przedstawionym na s. a, znajduje się w spoczynku. Jeśli linę AKB przetniemy w myśli po jednej i dru-?j stronie krążka K, to będą na nią działać siły S_x i S₂ przedstawione na rys. b. przypadku pomijalnie małych oporów tarcia na osi krążka, siły napięcia liny w częś-AK i części BK są jednakowe, tzn. S_t — S₂ = S (patrz zad * ^10X

J_, — -■» CT.w li cłin/<iin*a i>Ki<4ww    _

wanym położeniu (rys. a) ^znajduje się w spoczynku, zatem siły S_h S₂ i 0"tnuszą spełniać następujące równania równowagi:

= *S₂sina'—5'_łsina = 0,

I

^ P-,_y = cosa-J-5₂cosa' — O = 0.

Wobec równości sił: 5, — S₂ — S, z pierwszego równania wynika, że a' = a, tzn. że obydwa odcinki AK i BK liny tworzyć będą — w warunkach równowagi układu — jednakowe kąty a z pionowymi ścianami. Z drugiego równania — przy uwzględnieniu powyższych wniosków — otrzymujemy.

s = -2-.

2 cos a

Wartość kąta a znaleźć można z trójkąta ACE, w którym długość boku AC równa jest długości liny /, bok EC zaś określony jest wzajemną odległością ścian (rys. a). Z trójkąta tego mamy

CE a

^s,na ~ ca ~ r

VI²

a stąd

cosa = |/l— sin²a

Jak widać z powyższych wyrażeń, wartość kąta a zależeć będzie jedynie od długości liny / oraz odległości a między ścianami, natomiast zupełnie nie zależy od różnicy wysokości położeń punktów A i B. Znaczy to, że przy dowolnym położeniu punktu' zaczepienia A (np. punkt A') i każdym dowolnym położeniu punktu zaczepienia B (np. punkt B'), odcinki liny A'K' i B'K' będą zawsze nachylone do pionu pod kątem a (rys. a). W konsekwencji również wartości sił S napięcia liny będą dla stanów równowagi zawsze takie same, gdyż nie zależą od różnicy wysokości położeń punktów A i B zamocowania końców liny, a jedynie od jej długości / oraz odległości a między ścianami. Mianowicie

₅ Q Qi

2cosa 2]//²—a²

Pozostaje jeszcze do określenia położenie krążka K, odpowiadające stanowi równowagi. Zależeć ono będzie od długości odcinków liny w części AK i BK. Jeśli długość odcinka AK liny oznaczymy przez x, zaś odćinka BK liny — przez y, to do wyznaczenia ich wartości mogą posłużyć następujące zależności: x+y — Z, h— (y—x)co*ct_i

z których otrzymujemy

oraz

_ /cosa—h _ l{\fl²—a² —h) 2cosa    2}fi²—a²

iWF=s+h)