P3200167

262 4 AnaJiza bk. “Pień

i tworzy się pierwszą grupę z tych dwóch najbliższych sobie jednostek⁷⁴. Ta naj mniejsza odległość jest najniższym progiem podobieństwa (mówiąc obrazowo te dwie łączone jednostki są w najwyższym stopniu spokrewnione; związek I stop. niaj. W wyniku tego połączenia liczba skupień zmniejsza się z n do n — 1

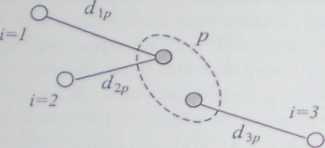
Rysunek 4.3. Zasada ustalania odległości w metodzie najbliższego sąsiada

Przed przystąpieniem do drugiego etapu łączenia należy określić odległości tego pierwszego (nowego) skupienia od wszystkich pozostałych skupień (na razie jednoelementowych) i uwidocznić je w macierzy odległości w wierszu r i kolumnie r (r poprzedza s) wyjściowej macierzy odległości D ^<0\ eliminując jednocześnie wiersz i kolumnę o numerze s. Zgodnie z kryterium najbliższego sąsiedztwa będą to mniejsze z dwóch odległości

= min(d_ir ,d_u)    (i = 1, 2,..., n; i & r; i s)    (4.93)

Przeliczanie odległości można wykonać według algorytmu

d„ =    - ^1 d_k - d_u I    (4.94)

Zauważmy, że jeżeli d_ir > d_is, to d_jp = d_lf. Jeżeli natomiast d_jr < d_js, to wówczas otrzymujemy d_ip = d_ir,d więc zgodnie ze wzorem (4.94).

W wyniku zastąpienia wyjściowych odległości w wierszu i kolumnie r odległościami przeliczonymi oraz usunięcia wiersza i kolumny s, otrzymujemy macierz odległości D^<n, która będzie punktem wyjścia do drugiego kroku. Następnie wyszukujemy kolejną najmniejszą odległość między inną parą obiektów i tworzymy nową grupę dwuelementową lub też dołączamy do istniejącej już grupy obiekt, jeśli jest on w stosunku do niego najbliższy. Procedurę tę powtarza się ite-racyjnie; po każdej iteracji obiekty są podzielone na coraz mniejszą liczbę skupień, aż do zgrupowania wszystkich obiektów w jednej grupie. Następujące po sobie poziomy grupowania ukazane są na dendrogramie.

75 Pamiętamy, że pierwszy krok w aglomeracyjnym grupowaniu hierarchicznym jest w każdej mc todzie identyczny.

pp"

Grupowanie hicrarchit/ne

4.6

Warto sobie uświadomić, ze w wierszu r oraz kolumnie r zostawianych w ma _cjerzy odległości I) “ zawsze wpisujemy mniejszy spośród dwóch odległości roz ważanych na danym etapie k, a następnie łączymy skupienia które mają na] mniejszą wśród wszystkich odległości Z uwagi na sposob przeliczania odległości metodę najbliższego sąsiada można scharakteryzować w ten sposób iż łączone są w niej te dwa skupienia, które mają minimalną spośród najmniejszych odległości (zob. rysunek 4.4).

/ O

• c

Rysunek 4.4. Odległość między skupieniami w metoć/.ic naibu/v.cg<, sąsiada

Odległości te są zaznaczane na dendrogramie i są określane jako poziomy łączenia. Poziome linie rysowane na dendrogramie które spinają dwa łączące się skupienia, nazywamy węzłami (ang. noda) Odstępy między dwoma kolejnymi węzłami, zaznaczane na dendrogramie w postaci linii pionowy ch, są nazy w ane m terwęzłami (ang. iniemodes) (zob. ry sunek 4 5 i dalsze

Jeżeli grupując metodą najbliższego sąsiada, opieramy się na macierzy podobieństwa, na przykład miarach typu korelacyjnego. to musimy pamiętać ze łącząc elementy w skupienia powinniśmy sic kierować największym podobieństwem czyli max{s„}. Podobnie przeliczanie podobieństwa w macierzy w każdym kolejnym kroku wymaga, aby relację (4.94) zastąpić relacią ; = minio . .s_t).

Przykład 4.3. (grupowanie hierarchiczne - metoda najbliższego sąsiada)

Wychodząc z następującej macierzy kwadratowych odległości euklidesowych między siedmioma obiektami, opisanymi pewną liczbą jednakowo mianowanych porównywalnych cech. przeanalizujemy metodę najbliższego sąsiada grupowania hierarchicznego:

0    4.23    3.50    7,64    5,11    4,05    2,75’

4,23    0    8,54    5.19    6,78    3,18    2,17

3,50    8,54    0    6.20    7.58    9,23    4.91

D¹⁰¹ = 7,64    5,19    6,20    0    4,17    4,22    5,72

5.11    6,78    7,58    4,17    0    2,51    8,37

4.05    3,18    9,23    4.22    2,51    0    5,65

275    2,17    4,91    5,72    8,37    5,65    0