s 184

184

7. Ruch plaski

Przyspieszenie punktu A₂ wyznaczamy składając trzy wektory    '^,_

stąd

aaj=^+<,o

Zadanie 7.28 Rozwiąż przykład 7.26, zakładając, że listwy poruszają się w przeciwnych kierunkach.

Odpowiedź

^aA₂ = Jai +

(ui + W2)⁴

16r¹

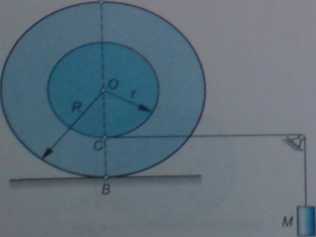
RYS. 7.46

aa =

a A = —-r^y/^aHR — r)¹ + v⁴

ac

Zadanie 7.29 Koło I o promieniu r, toczące się bez poślizgu po nieruchomym kole II o promieniu R, jest wprawiane w ruch za pomocą korby łączącej środki kół. Przyspieszenie chwilowego środka obrotu koła I jest w danej chwili równe a. Znaleźć prędkość kątową o> korby.

Odpowiedź

R(R +r)

Zadanie 7.30 Walec o promieniu R, toczący się bez poślizgu po prostej, jest wprawiony w ruch za pomocą ciężaru M. Ciężar jest przywiązany do końca nici, którą nawinięto na bęben o promieniu r (rys. 7.46). Wiedząc, że Vm = u, a*# = znaleźć przyspieszenie punktów A, B i C.

Wskazówka. Obliczyć najpierw przyspieszenie punktu O.

Odpowiedź v¹R

(R - r)¹ R

(R - r)

r2„2

(R - r)⁴

1

. (vi + U2)⁴

16r-