Scan Pic0330

168 Przykłady

Przykład 2.5. Wyznaczyć logarytm dziesiętny liczby pięcio-cyfrowej x = 1,7254.

Rozwiązanie. Ponieważ 100000 < 172540 <

< 200000, korzystamy z tablicy 2.1. W tablicy tej wartości mantys są podane tylko dla liczb czterocyfrowych. Wobec tego dla piątej cyfry należy wyznaczyć poprawkę p analogicznie jak w przykładzie poprzednim, przy czym różnica wynosi obecnie R = 25, a przyrost argumentu d = 0,0004. Ostatecznie otrzymujemy

Ig 1,7250 = 0,23679 (jak w przykładzie 2.3)

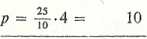
lg 1,7254 4 0,23689.

Przykład 2.6. Wyznaczyć logarytm dziesiętny liczby pię-ciocyfrowej x == 3,7283-

Rozwiązanie. Ponieważ2,0000 < 3,7283 < 9,9999,korzystamy z tablicy 2.2. Postępujemy analogicznie jak w przykładzie 2.4, przy czym poprawkę obliczamy w dwóch stadiach — najpierw dla czwartej, a następnie dla piątej cyfry liczby x. Otrzymujemy

, lg 3,7200 = 0,57054

Pi = -^-•8 =    93,6 (dla czwartej 'cyfry)

P2 = w'³ =    3,51 (dla piątej cyfry)

lg 3,7283 = 0,57151.

Uwaga 1. Zaokrąglanie mantysy do pięciu cyfr należy przeprowadzać w ostatnim stadium sumowania poprawek. Gdybyśmy zaokrąglali poszczególne poprawki to, jak to zachodzi w powyższym przypadku, może się zdarzyć, ^że suma zaokrągleń byłaby zbyt dużą.

Uwaga 2. Jak widać z przykładów 2.5 i 2.6, na wartość poprawek piątej cyfry mantysy wpływają również szóste cyfry liczby x. W przypadku więc x sześciocyfrowych nie należy liczby x zaokrąglać do pięciocyfrowej, lecz należy obliczać poprawkę również dla szóstej cyfry liczby x.

3* Wyznaczanie liczby x z danego logarytmu lgx

Przykład 3.1. Wyznaczyć x dla lgx = 1,20000.

Rozwiązań i e. Najbliższą tnniejszą mantysę od 20000 znajdujemy w tablicy 2.1. Ma ona wartość 19976 i odpowiada n b= 1584. Różnica mantys dla n = 1584 i n — 1585 wynosi R m 27 (podana w dolnej frakcji w wierszu 158 między kolumnami 4 i 5). Poprawka p = 20000-19976 = 24 odpowiada przyrostowi d m 10-    = 8,89. Ograniczamy się tylko do je

dnej cyfry poprawki, stanowiącej piątą cyfrę mantysy d = 9. Ponieważ cecha lgx jest równa jedności, więc 10 < x < 100. Ostatecznie

x = 15,849.

Przykład 3.2. Wyznaczyć x dla lgx — 1,98765.

Rozwiązanie. Bardzo bliską mantysę znajdujemy w tablicy 2.2, przy czym ma ona wartość 98767 i jest większa od podanej w zadaniu. Poprawka wynosi p = —2 dla różnicy R = 45. W tablicy tej mantysy są podane dla liczb trzycyfrowych. Dla jednostki cyfry czwartej poprawka wynosi w tym przypadku p_x =» — -jg-JR = 4,5. Dla jednostki cyfry piątej p₂ = - wt-R — 0,45. Poprawka p = —2 odpowiada więc przyrostowi dla piątej cyfry d —    = —4,44. Stąd ograni

czając się tylko do wyniku pięciocyfrowego

n m 97200—4 « 97196 oraz x - 97,196.