55592 Scan Pic0331

170 Przykłady

4. Obliczanie Iloczynów 1 potęg

Przykład 4.1. Obliczyć powierzchnię S elipsy o długości półosi a = 1,7254 cm, b = 3,7283 cm.

Rozwiązanie. Wzory : S = rtab, lgS = lg7c+ -ł-lga+lgó, zatem

lgn = 0,49715 (tablica 1) lg 1,7254 = 0,23689    (tablica 2.1 oraz przykład 2.5)

lg3,7283 = 0,57151 (tablica 2.2 oraz przykład 2.6)

lgS = 1,30555 S = 20,209 cm².

Przykład 4.2. Obliczyć objętość V kuli o promieniu R — =» 1,7254 cm.

Rozwiązanie. Wzory: K = j7cR³, lgK=lg(yw) + +3 Igi?. Logarytm współczynnika y w znajdujemy w tablicy 1. Logarytm liczby 1,7254 wyznaczamy z tablicy 2.1 (patrz przykład 2.5), lg 1,7254 — 0,23689. Ostatecznie otrzymujemy

lg(yTt) = 0,62209 (tablica 1)

31g 1,7254 * 0,71067

lgF — 1,33276 V - 21,516 cm³.

Uwaga. Wykorzystanie tablicy 1 może wydatnie przyspieszyć rachunki. Gdy w praktyce spodziewamy się częściej spotykać jakieś inne współczynniki, iloczyny itp., warto ich wartościami i wartościami ich logarytmów raz obliczonymi uzupełnić tablicę 1. Stanowi ona pamięć operacyjną naszych tablic analogiczną do pamięci operacyjnych maszyn liczących.

5. Obliczanie wzorów zawierających ilorazy Przykład 5.1. Obliczyć objętość V ostrosłupa, którego pod* stawa ma powierzchnię S — 21,571 cm², a wysokość h = = 17,215 cm.

Rozwiązanie. Wzory: V jŚh, lgF=—lg3+ H-lgS+lg/ł = lgj+lg5+lg/i, zatem

lg j = 1,52288 (podany pod tablicą 2.2) lg21,500 = 1,33244

lg 17,210 = 1,23578 p«-§.5=    12,5

lgK= 2,09265 V « 123,78 cm³.

liczby j podanego pod tablicą 2.2

Uwaga. W tym przypadku uniknięto obliczania kolo-garytmu przez wykorzystanie logarytmu często spotykanej

Przykład 5.2. Obliczyć promień R kuli o danej objętości V « 25,242 cm

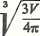
Rozwiązanie. Wzory: V» 4tcR³, skąd R =

gR = lg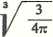+ ylgP, zatem

lg25,200 J 1,40140 lg25,242 = 1,40212