skan0041 (3)

44 Stany skupienia materii

2a:8. Butlę azotu o objętości 25 1 i ciśnieniu 2 atm podłączono do butli argonu o pojemności 50 1 i ciśnieniu 10 atm. Obliczyć ciśnienia cząstkowe oraz całkowite ciśnienie mieszaniny gazów po ich izotermicznym wymieszaniu. Odp.A-_ałk = 7,33 atm.

2a:9. Gęstość pewnego gazu w temperaturze 0°C i pod ciśnieniem 0,3 atm wynosi 2,0587 • 10^-3 g • cm^-3. Obliczyć masę cząsteczkową tego gazu.

Odp. M= 153,8 g • mol^-1.

2a:10. Wartości dtp dla C0₂ jako funkcja ciśnienia p w temperaturze 0°C wynoszą

p [atm]	1,00	0,50	0,1	0,01	0,001
d!p [g • dni^-3 • atm^-1]	1,9970	1,9702	1,9647	1,9635	1,9634

Obliczyć na tej podstawie masę cząsteczkową C0₂. Odp. 44,00 g • mol b 2b:l. Mając funkcję uwikłaną w postaci/(p, V, T) = 0, wykazać, że

2b:2. Wyprowadzić zależność

« / dp\

fi \ 377/

gdzie a oraz /? oznaczają odpowiednio izobaryczny współczynnik rozszerzalności cieplnej i izotermiczny współczynnik ściśliwości.

2b:3. Obliczyć współczynnik rozszerzalności termicznej a dla 1 mola: a) gazu idealnego, b) gazu Van der Waalsa. Odp.

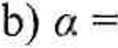
R

V{V-b)

1

RT _ 2a_ ' {V-bf V³

2b:4. Stałe a i b w równaniu Van der Waalsa dla etylenu wynoszą: a = = 4,47 • 10⁶ cm⁶ • atm • mol^-2, b = 57,1 cm³ • mol^-1. Obliczyć objętość jednego mola etylenu w temperaturze 298 K i pod ciśnieniem 10 atm, stosując: a) równanie stanu gazu idealnego, b) równanie Yan der Waalsa. Odp. b) 2,314 • 10^-3 m³ • mol^-1.

2b:5. 1 mol ^-oktanu w temperaturze 400°C i pod ciśnieniem 1 atm (stan 1) sprężono do ciśnienia 20 atm (stan 2) i schłodzono pod tym ciśnieniem do 300°C (stan 3). Obliczyć objętość w tych stanach, stosując: a) równanie stanu