skanowanie0003 (232)

86 I

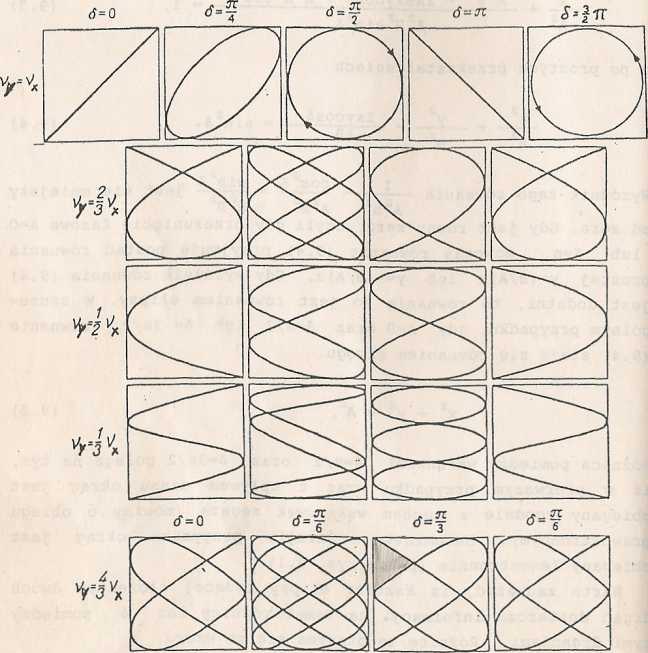
Rys. 9.1. Figury Lissajous pochodzące ze złożenia wzajemnie

prostopadłych drgań harmonicznych o jednakowyca

amplitudach lecz różnych częstotliwościach ( v , v )

x y i

i różnych wartościach różnicy faz 6 pomiędzy nimi"B

Jeżeli częstotliwości drgań harmonicznych wykonywanych w kierunkach wzajemnie do siebie prostopadłych nie są równe, ale stosunek ich jest liczbą wymierną, to w wyniku złożenia tych drgań uzyskujemy bardziej lub mniej skomplikowaną krzywą zamkniętą zwaną figurą (krzywą) Lissajous (rys. 9.1). Postad

krzywych Lissajous komplikuje się coraz bardziej, gdy stosunek częstotliwości wyraża się coraz większymi liczbami całkowitymi. Istotne jest jednak to, że wszystkie te krzywe mieszczą się w prostokącie o bokach równych

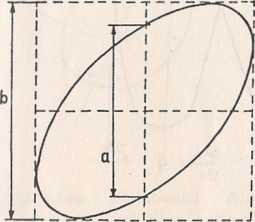
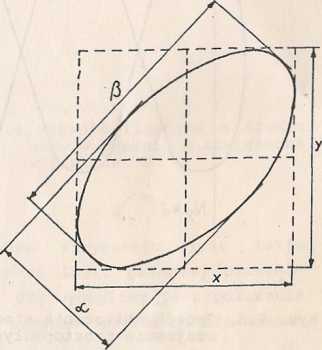
Rys. 9.2. Określenie parametrów elipsy Lissajous wykorzystywanych we wzorach (9.6) i (9.7) do wyznaczenia różnicy faz pomiędzy dwoma wzajemnie prostopadłymi ruchami drgającymi o tej samej częstotliwości

podwojonym amplitudom drgań składowych. Poza tym stosunek częstotliwości drgań składowych można łatwo obliczyć ze stosunku liczby przecięć prostej pionowej z krzywą Lissajous do liczby takich przecięć prostej poziomej (rys. 9.3)

Vk

JL_ =

N..

(9.8)

V    N |

x    y

-_x, Ny oznaczają liczby przecięć krzywej Lissajous odpowiednio z prostą równoległą do osi X oraz z prostą

gdzie N_. odpowi równoległą do osi Y

v

v_y oznaczają częstotliwości drgań

wzdłuż osi X i Y.

Należy zwrócić uwagę, iż proste wykorzystywane do obliczenia stosunku częstotliwości powinny być tak prowadzone', aby nie były styczne i nie przechodziły przez punkty węzłowe krzywej Lissajous.