skanuj0002 (356)

Hrcdzisr V

w dalszej części wykładu okaże się, że nasze próbki żywności, lakie jak pieczywo czy wypieczone ciasto, też go nie spełniają. Należy lu wyjaśnić, że zasada kontinuum stanowi fundament spójności opisu matematycznego: Spróbujmy sobie bowiem wyobrazić definicję pola powierzchni w przestrzeń; dyskretnej (punktowej).

W odniesieniu zaś do rzeczywistych materiałów bardziej chodzi nam o ich makroskopową jednorodność, czyli o to, żeby pęcherzyki powietrza w wypieczonym cieście były^-jednakowe, niż o ścisłe zachowanie ciągłości materii występującej wszakże w surowym cieście lub w zakalcu.

Pewnym pocieszeniem może być fakt, iż. w teorii sprężystości i plastyczności. posługującej się nieporównanie bardziej skomplikowanym aparatem matematycznym, zasada kontinuum jest wręcz niezbędna do formalnie poprawnego wyprowadzenia kluczowych równań.

Na gruncie wytrzymałości materiałów będziemy więc pamiętać, żc ciała traktujemy jako ciągle, ale raczej w sensie makroskopowym.

Podstawowe pojęcia

Oddziaływania wewnętrzne. W przedmiotach z zakresu mechaniki ciała stałego wprowadzamy dwa rodzaje oddziaływań wewnętrznych - objętościowe i powierzchniowe. Objętościowe to np. siły ciężkości (masa zanu-izona w pulu grawitacyjnym), powierzchniowe te np. ciśnienie oraz naprężenie. Należy podkreślić zasadniczą różnicę między zarówno sposobem realizowania się. jak i skutkami działania obydwu rodzajów oddziaływań. Pierwszy - objętościowy - to oddziaływania dalekiego zasięgu, mające bezpośredni wpływ na dowolną część materiału. Można powiedzieć, żc działają one „na wskroś" prze z materiał (tak jak grawitacja). Są one realizowane wtedy, gdy ciało mające pewną własność (masa) jest zanurzone w polu działającym na tę własność (grawitacja). Ponieważ pole działa na dowolną część materii ciała, każda jego część jest poddana sile ciężkości. Należy zauważyć, że jeżeli pole jest jednorodne, a ciało swobodne (nie podparło), to oddziaływania objętościowe oprócz przyspieszenia nic wywoląją żadnych odkształceń. Ciężar nie jest jedyną siłą objętościową, należą <lo nich tnkzc oddziaływania elektrostatyczne, magnetyczne oraz elektromagnetyczne (np. wzbudzenie drgań w cząstkach materii pod wpływem zmiennego pola elektromagnetycznego realizowane w kuchni mikrofalowej). W wytrzymałości materiałów oddziaływania objętościowe są nu ogół pomijane.

Drugi - powierzchniowy to oddziaływania bliskiego zasięgu mające bezpośredni wpływ na bardzo ograniczony obszar. Należą do nich np, ciśnie-nic czy naprężenie. które zostanie zdefiniowane w dalszej części wykładu. Należy przy tyra zwrócić uwagę na fakt. ze potoczne rozumienie .obciążę nia~ dowolnego ciab (ckmemu) jest realizowane właśnie przez siły powierzchniowe. Na przykład, talerz obciąża W a siołu przez naciskanie dolną krawędzią na powierzchnię blatu, krzesło obciążą podłogę (strop) naciskiem czterech (na ogól) nóg na jej powicrzdtnię. Zauważmy ze zgodnie z zasadą Sam VenantH generalny rozkład sil wewnętrznych w stropie nic za leży od liczby nóg krzesła, a jedynie od jego ciężaru.

W badaniach wytrzymałościowych obciążenia próbek realizowane są tez powierzchniowo. Jakkolwiek, korzystając / zasady Sam Veminta wiemy, że próbka będzie zachowywać się tak samo niezależnie od niedokładności jej zamocowania, to właśnie sposób zamocowania nastręcza sporo trudności. Na pr/yklad. przy próbie rozciągania złe zamocowanie powoduje zerwanie próbki tuz przy uchwycie, co dyskwalifikuje próbę.

Naprężenia. Pojęcie naprężeń jest jednym z elementarnych w wytrzymałości materiałów.-Jest (ak podstawowe w całej mechanice ciała stałego jak siła w fizyce i podobnie abstrakcyjne. Wyobraźmy sobie silę przyłożoną do pewnej powierzchni, np. naciskamy palcem na powierzchnię stołu. Jeżeli teraz podzielimy przykładaną siłę przez wielkość powierzchni, utrzymam właśnie liczbową wartość naprężenia. Będzie to tzw. naprężenie średnie. Naprężenie w punkcie definiujemy jako granicę ilorazu siły i powierzchni przy założeniu, że wielkość powierzchni dąży do zera:

a « —— gdzie AS-*0 AS

Jak widać, naprężenie ma miano ćmienia. czyli MPt. Podobnie jak siła jest wielkością wektorową, tak naprężenie jest wielkością tensorową. To znaczy, żc w dowolnym układzie współrzędnych opisane jc$t *kfack*wynu. Jednakże jeżeli siła ma w układzie trójwymiarowym trzy składowe, te naprężenie ma ich dziewięć, z których sześć jest niezależnych. Ponieważ wektor siły V⁷ może byc przyłożony do powierzchni AS pod dowolnym kątem, więc* we współrzędnych prosiokąinycfc. przyjętych tak. ze oś X jes* prostopadła do AS i skierowana na zewnątrz rozpatrywanego ciała. a osie Y i Z leżą na AS. wektor siły AT można opisać trzema współrzędnymi Af\. AFf AF/. Zgodnie t cytowanym powyżej wzorem otrzymujemy:

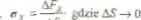
AS