skanuj0024 (118)

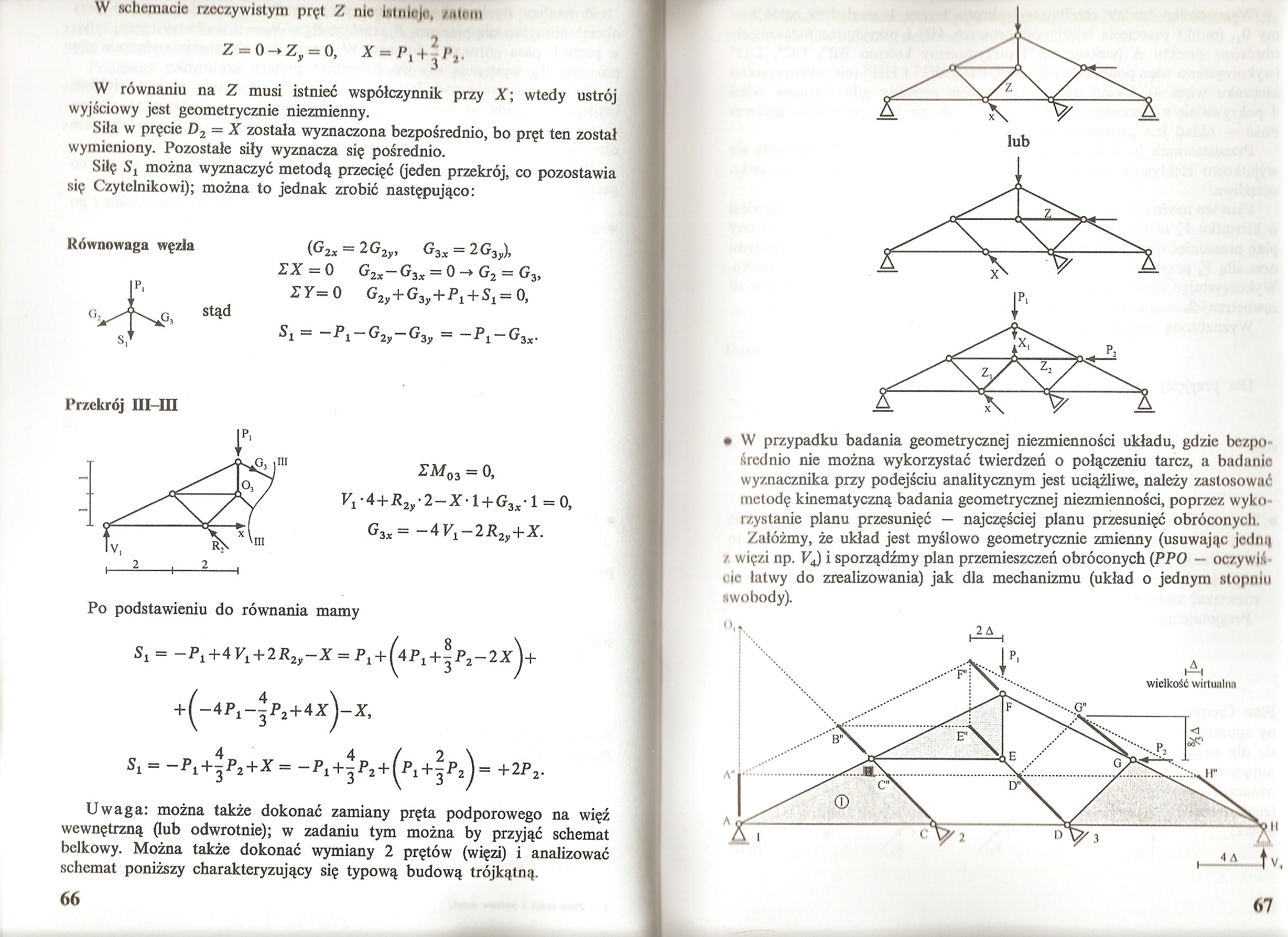
W schemacie rzeczywistym pręt Z nie istnloje, /ulom

z = o-*z, = o, * =

W równaniu na Z musi istnieć współczynnik przy X; wtedy ustrój wyjściowy jest geometrycznie niezmienny.

Siła w pręcie D₂ = X została wyznaczona bezpośrednio, bo pręt ten został wymieniony. Pozostałe siły wyznacza się pośrednio.

Siłę Si można wyznaczyć metodą przecięć (jeden przekrój, co pozostawia się Czytelnikowi); można to jednak zrobić następująco:

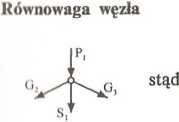
(G_2x — 2 G_2yt G_3x = 2G_3y),

ZX = 0 G_2x—G_3x = o -> g₂ = g₃, ZY= 0    G₂,+G3,+P₁+S₁= 0,

Si = ~Pi~G_2y~G_3y = —P i~-G_3x.

Przekrój ni-m

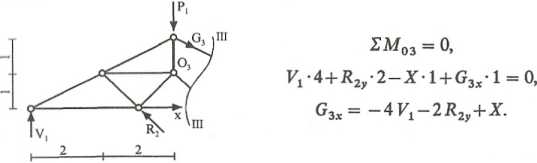
Po podstawieniu do równania mamy

= -P_l+4V_l+2R_2v-X = P₁+^4J>₁+|p₂-2X^+

+(-⁴i^,i-|p₂+⁴^)-X_>

«i = -P₁Ąp₂+X= -P₁₊lp_{2 +} ^₁₊|j>^= +2P j.

Uwaga: można także dokonać zamiany pręta podporowego na więź wewnętrzną (lub odwrotnie); w zadaniu tym można by przyjąć schemat belkowy. Można także dokonać wymiany 2 prętów (więzi) i analizować schemat poniższy charakteryzujący się typową budową trójkątną.

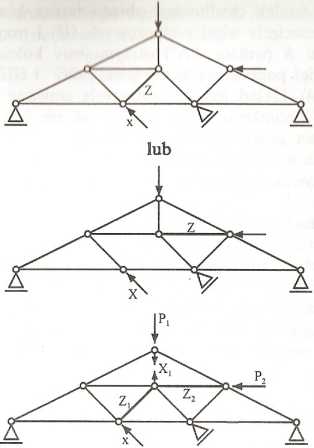
• W przypadku badania geometrycznej niezmienności układu, gdzie bezpośrednio nie można wykorzystać twierdzeń o połączeniu tarcz, a badanie wyznacznika przy podejściu analitycznym jest uciążliwe, należy zastosować metodę kinematyczną badania geometrycznej niezmienności, poprzez wykorzystanie planu przesunięć — najczęściej planu przesunięć obróconych.

Załóżmy, że układ jest myślowo geometrycznie zmienny (usuwając jedną z więzi np. KJ i sporządźmy plan przemieszczeń obróconych (PPG — oczywiście łatwy do zrealizowania) jak dla mechanizmu (układ o jednym stopniu swobody).

67