skanuj0079 (30)

138 B. Cieślar

ganię i na ściskanie, a także y^yd, musimy projektowanie przeprowadzić dla największego momentu zginającego: zarówno dodatniego, jak i ujemnego.

138 B. Cieślar

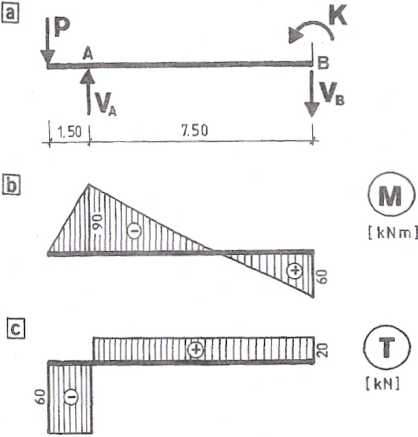
Rys. 4.4.2

-=18t⁴.

Obliczamy moment bezwładności: 3t(6t)³

36

Projektowanie w przekroju o największym momencie ujemnym M = -90 kNm:

_{Oi=Or =} 90J0^2t<f ,₆; ^{1 r} 18t^{4 dr}

(D

t> 0,1186 m;

a₂ = Oc=20J0^4t^_{f    15;}

18t⁴

t S 0,1101 m.    (2)

Projektowanie w przekroju o największym momencie dodatnim M = +60 kNm:

_{Ga =} o_r=60J0lJt_Sf -₆;

a r    _18t4    dr I

_ 60-10"³-2t

^f_dc=15;

18f

t > 0,0763 m.    (4)

Warunki (1),(2),(3) i (4) spełnia parametr t > 13,05 cm.

Warto tutaj zauważyć, iż przekrojem niebezpiecznym, tzn. takim, w którym naprężenia najszybciej osiągną wytrzymałość obliczeniową, okazał się przekrój, w którym działa mniejszy, co do wartości bezwzględnej, moment zginający (M = 60 kNm).

Przyjmując t = 14 cm otrzymamy naprężenia normalne rzeczywiste o wartościach przedstawionych na wykresach z rysunków:

4.4.3a dla M = -90 kNm; 4.4.3b dla M = +60 kNm.

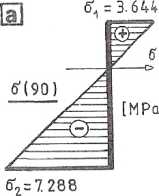
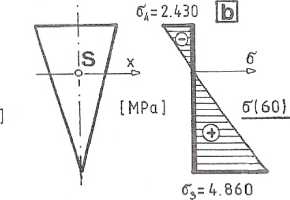
Rys. 4.4.3

W powyższym zadaniu projektowanie przekroju można było znacznie skrócić, zauważywszy zależności:

<Ł	_^2	_ 90
<>4		"60
2*.	_£ł	_4t
	<*4	2t

do których podstawiamy bezwzględne wartości naprężeń. Przyjmując np. 03 = f* = 6 MPa, czyli wartość dopuszczalną, łatwo stwierdzić, iż 04 = 3 MPa, 01 = 4,5 MPa, 02 = 9 MPa. A zatem każde z naprężeń jest mniejsze od stosownej wytrzymałości obliczeniowej. Rozwiązaniem układów nierówności (1), (2), (3) i (4) będzie więc parametr „t”, otrzymany z rozwiązania nierówności (3). Gdybyśmy analizę rozpoczęli od przyjęcia 02 = 15 MPa, otrzymalibyśmy wartość ci = 7,5 MPa, czyli większą od fdr = 6 MPa. Wskazany sposób postępowania możliwy jest do zastosowania również i w innych zadaniach.