78799 skanuj0091 (30)

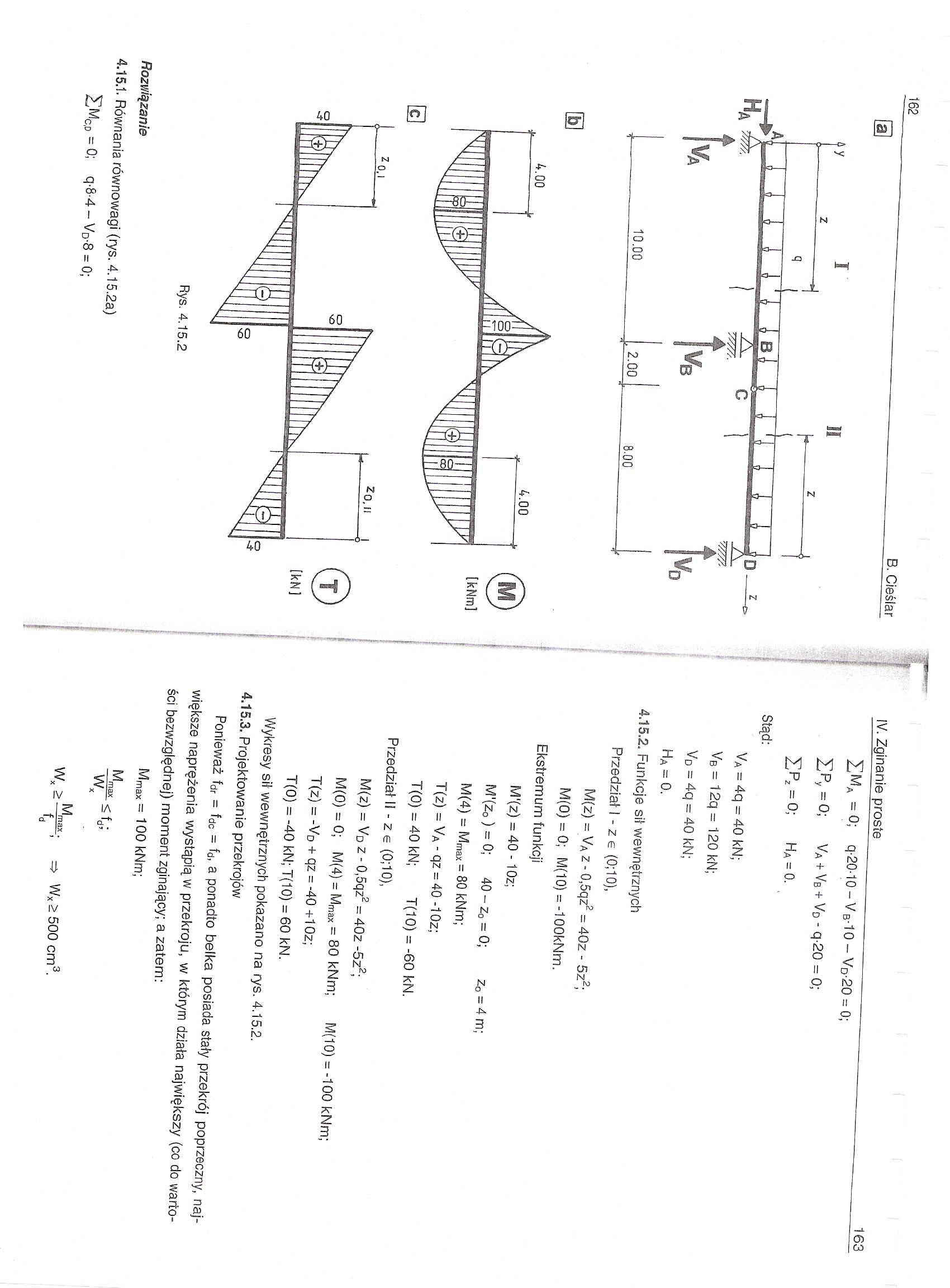
162 B. Cieślar

S

l	y	i ^2 j				11 1- z
		^q i				r JL
	1	rrrr	i A Bi j			rri i	j	D ^z p
ha		[	JtE 'TTTP/.		c	1	1 W Ł	E & i
	k			VB			^1	VD
		10.00		. 2.00		8.00		.

Rozwiązanie

4.15.1. Równania równowagi (rys. 4.15.2a) £^mc,d=0;    q-8-4 - V_d-8 = 0;

IV. Zginanie proste__

163

£M_a =0; q-20-10 - V _B-10 - V_D-20 = 0;

£P_y=0; V_A + V_B + V_D - q-20 = 0;

2]Pz = 0;    H_a=:0.

Stąd:

V_A = 4q = 40 kN;

V_B = 12q = 120 kN;

Vq = 4q = 40 kN;

H_a = 0.

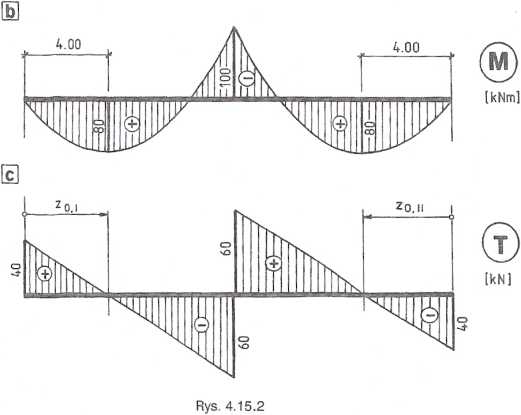
4.15.2. Funkcje sił wewnętrznych Przedział I - z e (0;10),

M(z) a V_A z - 0,5qz² = 40z - 5z²;

M(0) = 0; M(10) = -100kNm.

Ekstremum funkcji M'(z) = 40-1 Oz;

M'(Zo) = 0;    40 - z₀ = 0; z₀ = 4 m;

M(4) = M_max = 80 kNm;

T(z) = V_A - qz = 40 -1 Oz;

T(0) = 40 kN; T(10) = -60 kN.

Przedział II - z e (0;10),

M(z) = Vd z - 0,5qz² = 40z -5Z²;

M(O) = 0; M(4) = Mmax = 80 kNm; M(10) =-100 kNm;

T(z) = -V₀ + qz = -40 +1 Oz;

T(O) = -40 kN; T(10) = 60 kN.

Wykresy sił wewnętrznych pokazano na rys. 4.15.2.

4.15.3. Projektowanie przekrojów

Ponieważ f_dr = f_dc = f<j. a ponadto belka posiada stały przekrój poprzeczny, największe naprężenia wystąpią w przekroju, w którym działa największy (co do wartości bezwzględnej) moment zginający; a zatem:

Mmax =100 kNm;