spomK 01

SYSTEMY POMIAROWE 2 - SPRAWDZIAN 010123
Zadanie 1 4 pkt
Wyznaczyć wariancję estymaty p parametru /), modelu y - p0 + ptx, otrzymanej metodą
adiatów na podstawie danych
|
n |
r n |
-V„ |
|
1 2 3 |
6 1 4 |
4 0 4 |
najmniejszych kwadratów na podstawie danych
2 I 0 u
3 __4__4
wiedząc, ze macierz kowariancji błędów tych danych ma postać:
•10 •'
3 2 0 2 2 1 0 I 2
Rozwiązanie: Zgodnie ze wzorem (6.18) układ równań normalnych ma w tym wypadku postać: 3/>o + H/>, = yt+y2 + v3 11 A, + 53/>, = 6 yt + >2 + 4 j/3 Błąd jego rozwiązania wyraża się wzorem
L-*
y2 -y2 l3-y3
£,-A ssi(72i“8Ł+Ł)"^(7^,-8>'2+>',) = ^[7 -8 l]7
a w konsekwencji:
|
v4t>, |
K£ |
I e[(p |
.-/ó)2] |
|
Varl£, |
j= 2.56 |
•I0"6 |
|
7 |
'3 2 0' |
7' | ||
|
8 l]% |
-8 1 |
i oc |
2 2 1 0 1 2 |
-8 1 |
- Zadanie 2 6pkt
Do wzorcowania pewnego toru pomiarowego, którego modelem jest zależność y- P\X, + p2x2, zastosowano metodę najmniejszych kwadratów - zakładając, że plan eksperymentu ma postać:

Wyznaczyć wartość parametru a, dla której suma wariancji estymat parametrów p{ i p2 jest największa.
Rozwiązanie:
A = XrX = U,
yb.ye(l,2}
Au =4 +a2, An =A2] =2a-l, A22 =4 +a2
det(A)=(4+a2)2 -(2a-l)2 =16 + 8a2 +aA -a4-4a2 -4a-l = 15 + 4a + 4a2 +a4
A11 + ^22
det(A)
bo A-1
1_
det(A)
A 22 - A2i
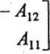
Wyszukiwarka
Podobne podstrony:
spomK 02 SYSTEMY POMIAROWE 2 - SPRAWDZIAN 001211 Zadanie*: 4 pkt Wiedząc, że surow
XXX (3) SYSTEMY POMIAROWE 2 - SPRAWDZIAN 010306 Zadanie 1: 1 pkt Zdefiniować jedny
linda (2) SYSTEMY POMIAROWE 2 (SPOM2) - SPRAWDZIAN 000418 Zadanie 1: 6 pkt Wyznacz
11152 Kolos2 1 SYSTEMY POMIAROWE 2- SPRAWDZIAN 010320 Zadanie 1: Zbadać, czy następująca macierz jes
img007 (51) SYSTEMY POMIAROWE 2 - EGZAMIN 000615 Zadanie 1 7 pkt Zdefiniować jedny
spomK 08 SYSTEMY POMIAROWE 2 (SPOM2) - SPRAWDZIAN 000104 Zadanie 1: 1 pkt Zdefinio
spomK 07 SYSTEMY POMIAROWE 2 (SPOM2) - SPKAWU/.1AIN (JUU4I8 Zadanie 1: &nbs
spomK 18 >VM iuvi v roiMlAKOWK 2 (Sl*OM2) - SPRAWDZIAN 000104 Zadanie 1: 7 pkt
więcej podobnych podstron