linda (2)

SYSTEMY POMIAROWE 2 (SPOM2) - SPRAWDZIAN 000418

Zadanie 1:    6 pkt

Wyznaczyć przedział rozrzutu estymaty niezurandu zdefiniowanej wzorem:

3- = h ■ P\'y ^! pi)’¹

gdzie p₀ - 1 , />:    1 i p, ■    -1 są estyrnatami parametrów wyznaczonymi podczas wzorcowania, a

y - 1 surowym wynikiem pomiaru. Założyć, zc adekwatnym modelem matematycznym błędów estymacji parametrów są identyczne niezależne zmienne losowe o rozkładach równomiernych w przedziale I • 0.1. rO.lj, zaś adekwatnym modelem matematycznym błędu surowego wyniku pomiaru - znr.mma losowa o rozkładzie równomierny w przedziale. [- 0.2, -t- 0.2j, niezależna względem zmiennych losowych modelujących błędy estymacji parametrów.

Rozwiązanie:    W pierwszym przybliżeniu wpływ błędów parametrów i surowego wyniku pomiaru

na błąd estymaty niezurandu określają pochodne cząstkowe tej estymaty dla p₀ = 1 , p, — 1,

P2=~ i ¹ y =^1:

OX    c w’    C/X    ^ óx

OP₀    C T ’ •    {sl?-)    C/J?

Informacja ta pozwala dobrać odpowiednie kombinacje skrajnych wartości parametrów i surowego wyniku pomiaru, którym odpowiadają skrajne wartości mezurandu:

— inf "me. * = Po	^f -i pfr^up+pf [y^sup]^2 =0-396
x^sup = Pq"	- : p^y'^M + p2^Up[y’^nf]^2 = 1.404
Przybliżenie linio\	ve daje przedział x e[o.6,1.4], co w pewnych sytuacjach pomiarowych nic	może
być uznane za wia	r,'godne oszacowanie niepewności.	A
Zadanie 2:		‘i pkt

Do estymacji parametrów p₀ i p, modelu tom pomiarowego:

y-Po + p\^x\

metodą najmniejszy'-¹- kwadratów zastosowano plan eksperymentu:

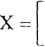
oraz dane pomiarowe y = [?.l    1 -1 19 21 -lj . Wyznaczyć estymaty parametrów p₀ i p,

oraz estymatę wariancji pojedynczego wyniku pomiaru.

Rozwiązanie: Układ równań normalnych ma postać:

6	()	Po		60"
0	6	_Pt.		62

.    .    I

co oznacza, żc estymaty parametrów mają wartości: p₀ = 10 i p, -10-. Odpowiadająca im prognoza wartości wielkości wyjściowej - to:

u ii <>>	1 1 1 20- - -L 3 3 3	1 1 ll 20- 20- --3 3 3J	T > stąd: y - y =	'2 3	4 2 3 3	4 2 2' ~ 3 3 3.
llv vlf	48 „2	^1 11 rr cl	CC 1 fN	4
II ^ y|i2	9 ^Gy ~	1 1 V • 1	^2 6-1-1 9 "	3