12456 spom egz01

SYSTEMY POMIAROWE 2 (SPOM2) - EGZAMIN 990203

Zadanie I: Zdefiniować jednym zdaniem każde z następujących pojęć:

•    wzorcowanie toni pomiarowego,

® przedział ufności estynąąty .wyniku pomiaru,

•    równanie normalne,

•    ortogonalny pl Ji eksperymentu,

•    D-optymaLny plan eksperymentu.    .    <    7pkl

\

Zadanie 2: Wyznaczyć funkcję gęstości prawdopodobieństwa opisującą rozkład błędu odtwarzania rnezurandu według wzoiu:

x = 0.5 y + 02v

gdzie y jest surowym wynikiem pomiaru, obarczonym błędem o rozkładzie równomiernym w

przedziale

rozkładzie równomiernym w przedziale [-5,+5].

estyrnatą wartości wielkości wpływającej, obarczonej błędem o

6 pkt

Rozwiązanie: Badany estymator ma postać:

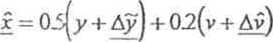
Ai = 0_5Ąy + 02 Ay

skąd wynika, że:

. Zmienna losowa z, = 0_5Ąy ma rozkład równomierny w przedziale [—10,+10], zmienna losowa

v

z, = 02Ay ma rozkład równomierny w przedzialea zatem funkcja gęstości

prawdopodobieństwa f(x) opisująca rozkład Ax wyraża się splotem następujących funkcji:

Jest wiec:

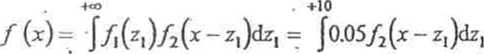
-10

-co

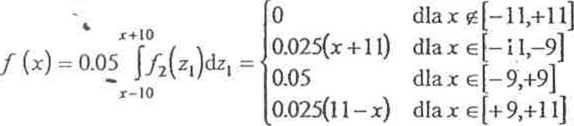
Zadanie 3: Do estymacji parametrów p_], p₂ i p₃ modelu toru pomiarowego:

y = p_lx_i+p₂x₂+p_ix_i

'zastosowano metodę najmniejszych kwadratów i pian eksperymentu:

•«v    1-1    1-1    1-1    1-a

X^r=    1 -U    -1 a    I -1    -1    1

a 1    1 i    -1 -1    -I -1

a) Dla jakiej wartością a-a suma kwadratów współczynników korelacji estymat p_}, Pi ¹ Pi osiąga minimum ? ♦