str064 (3)

m mwt ly

«, I '    (5.31)

Juk wynika z zależności (5.28) oraz (5.31) obn współczynniki refrakcji różnią się jedynie zna-klom. Przyjmując przybliżone oszacowanie współczynnika r , postaci

e, = -40.3 • N_e ,    (5.32)

windy współczynniki refrakcji jonosferycznej dla pomiaru fazy oraz kodu można określić z pierwszym, wystarczająco dokładnym, przybliżeniem:

pomiary fazowe:    40 1 Af

»„=1--JT^    •    (5-33)

pomiary kodowe:    40 3 N

*,=! + - 'p ‘    •    (5-34)

Annli/n równań (5.33) i (5.34) prowadzi do przytoczonego wcześniej wniosku, iż: n,_f < n_g oraz v_(! v,_(l Potwierdza to istnienie różnicy między prędkościami rozchodzenia się sygnału kodowego (opóźnionego) i fazowego (wyprzedzonego).

5.2.4. Opóźnienie jonosferyczne

Opóźnieniem jonosferycznym sygnałów GPS - A, jest różnica między geometryczną I mlmkcyjną drogą sygnału. Zdefiniujmy, zmierzoną (    ) oraz geometryczną ( r,) odległość

mli,ulży satelitą a odbiornikiem

Pj ⁼ J wdp./ i    (5.35)

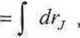
(5.36)

gil/lo ii jest współczynnikiem refrakcji.

/miwaźmy przy tym, że w przypadku, gdy współczynnik refrakcji zmienia się w sposób ciągły li i lula elektromagnetyczna wybierze trajektorię wzdłuż odległości p ₇ taką, że czas potrzebny nu jej przebycie będzie najkrótszy. W tym wypadku droga ta przyjmie kształt paraboliczny. Wyznaczając wartość Aj w oparciu o (5.35) i (5.36) otrzymamy:

&j=Pj-rj=\ndpj-$drj.    (5.37)

Podstawiając w miejsce n , zależności na grupowe i fazowe współczynniki refrakcji ze wzorów (5.28) oraz (5.31), otrzymamy wzory opisujące fazowe oraz grupowe opóźnienie jonosferyczne:

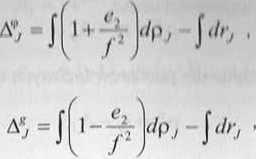
(5.38)

(5.39)

gdzie:

Af, - fazowe opóźnienie jonosferyczne,

A⁸j - grupowe (kodowe) opóźnienie jonosferyczne.

Po całkowaniu pierwszych wyrazów zależności (5.38) i (5.39) otrzymamy:

A>J ^drj.

A*=-J    (6.4D

Albowiem przyjęliśmy oszacowanie przybliżone (5.32), wtedy

^=-jr\^NAj .    (B.3D

40.3 _f „ ,

A^gj=-j_r\Ndr_J .    (6 12)

Uwzględniając definicję TEC z (5.1) otrzymamy alternatywną postać:

»    40 3

A ^-7EC,    (5,33]

40.3

A^gj=yfTEC.    (5.34]

Jeśli przyjmiemy, pomijając znak, że wartość poprawki jonosferycznej dla pomiarów kodo wych wyniesie

A,=

40.3

f²

TEC

(5.35;

132