str065 (2)

windy poprawioną o In poprawkę | >nt n tcli u u lir <( |lf tńt dln pumlitrów kodowych wyrazimy juko

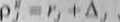
(5.36)

u przyjmując analogiczne założenie dla pomiarów la/owych otrzymamy

(5.37)

Pj =0 a₇ .

W /istosowaniu praktycznym modelowaniu podlega wertykalna liczba elektronów - TVEC (nim Folnl Vertical Electron Content), która odnosi się do zenitu obserwatora. Dzięki temu możliwym staje się uwzględnienie chwilowej wysokości topocentrycznej satelity i obliczenie opóźnienia jonosferycznego wzdłuż każdej z tras sygnałów, wtedy:

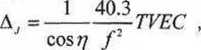
(5.38)

gd/lo /redukowana odległość zenitalna r) jest wyznaczona z zależności

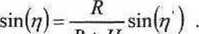
R + H

(5.39)

Wo wzorze (5.39) wartość R odpowiada średniemu promieniowi Ziemi, zmienna H jest wysokością pojedynczej warstwy z zakresu od 350 do 450 km, natomiast współczynnik —!— odwzorowuje dowolny kierunek obserwacji w stosunku do zenitu obserwatora.    ^C0ST) fi 7.5 Algorytm Klobuchar’a

W 1986 roku J. Klobuchar opublikował algorytm obliczenia opóźnienia jonosferycznego dln użytkowników systemu GPS pracujących w oparciu o jedną częstotliwość oraz pomiary kodowo. Użytkownicy kodu C/A, w oparciu o niniejszy model oraz dane transmitowane w 4 pod-i • ni u «i depeszy satelitarnej GPS, mogą przeprowadzić redukcję opóźnienia jonosferycznego. Modni ten został opracowany na podstawie wcześniejszego modelu Bent’a. Algorytm Klobu-i lwim /układa szereg uproszczeń, które decydują o możliwości redukcji opóźnienia jonosfe-ryo/nogo do poziomu ok. 50 %. W ogólnej postaci rozważany algorytm określa opóźnienie Jonrmforyczne zgodnie z zależnością

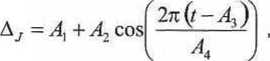
(5.40)

Ijd/lo wartości poszczególnych współczynników wynoszą

(5.41)

A, =5-10 ⁹s = 5ns

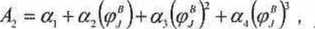
(5.42)

A, - fl_x + (i_} {<p",)+    )' i //₄ (K)' .    (5.44)

Pozostałe zmienne to

a,, - współczynniki reprezentujące amplitudę opóźnienia w płaszczyźnie wertykalnej modułu, jS_n - współczynniki reprezentujące okres rozważanego modelu,

LT - czas lokalny,

(p^Bj - kąt pomiędzy punktem wejścia sygnału w jonosferę, a osią magnetyczną Ziemi mierzony po kole wielkim.

We wzorze (5.40) parametr t reprezentuje czas lokalny miejsca obserwacji

t = yj + tjjf ,    (6>4B)

gdzie:

Xj - długość geomagnetyczna punktu wejścia sygnału do jonosfery, t_UTC - czas UTC.

Stałe (p_s,A,_B są współrzędnymi położenia bieguna magnetycznego (przybliżono wartości) wynosząc

9_ł = 78*JV,    >.,=291 ‘E,    (5.46), (5.47)

wtedy parametr cp^sj obliczyć można z zależności

cos sin((p_J )sin(cp_B )+ cos((p, )coscp_fl (>_v - X₈ ) ,    (5.4B)

w której <p^B; jest szerokością geomagnetyczną punktu wejścia sygnału do jonosfery.

Wartość opóźnienia jonosferycznego wymaga odniesienia jej do wysokości topocen trycznej satelitów poprzez odwrotność funkcji cosinus wysokości zenitalnej. W efekcie otrzymujemy wartość nanosekund (10-150 ns), która po przemnożeniu przez ustaloną dla GPS prędkość fali elektromagnetycznej (c=2.99792458 • 10⁸m s¹) pozwoli otrzymać odległość, o którą należy poprawić wynik pomiaru pseudoodległości do danego satelity.

135