wah3

VIII Ruch drgający

2.13. Dane:

A--i

fi~ 2

Szukane:

/,=

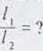
¹ 2317/

/? = /I

1

i'	f\ =	g
43t^2/, ’		47t^2/
X	4 TI^2/
4/T/2	g	l2

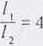
2.14. Dane:

A 7'= 0,2 s

Szukane:

/,= ?

2.16. Dane: L

Szukane: 7 = ?

cl -ijl. - odległość środka masy (śni.) od osi obrotu. Moment bezwładności pręta: / = l    md'

= -py m L² + m ^ If j = -py m I: + ^ m L² = -py m L?= ^ m V

7'= 231

maci

ml: 2 3 ma /-

2L 3 g

Rozwiązania

oś

Ryc. 8 15

2.17. Dane:

7) = 7',= r, L

Szukane:

/=?

1 = 4

I

T = T₂-AT=2T_rAT - AT=T,

. I _ 1 _ 1 I _ _g 1 _r ^y i r, ^_ AT ”0,2s'³s'^{3 mz}

I

Okres wahań pręta wyznaczony jest w rozwiązaniu zadania 2.16: Okres wahań wahadła prostego: 7’= 2 31 Okresy tych wahań mają być jednakowe:

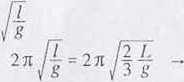
T= 271

l

g

salto

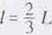
Tę długość / zastępczego wahadła prostego nazywamy długością zredukowaną wahadła fizycznego.

2.18. Dane:

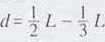
Szukane: T= ?

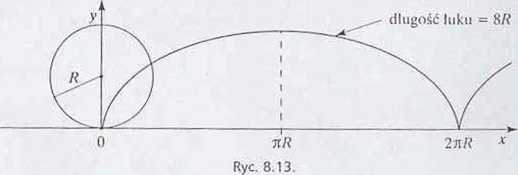
2.15. Jesl to możliwe, jeżeli kulka wahadła będzie się poruszać po linii zwanej cykłoidą. Cykloidę zakreśla punkt leżący na kole, które toczy się po płaszczyźnie (ryc. 8.13).

‘<=i ^L-^^L=i^L-i^L=l^L

2

7= I _n -i -md' - py m I: + m | p /. j = -p, m /. + ^ m Lr= -jg m l: = ^ m I:

T=2n

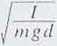
= 271

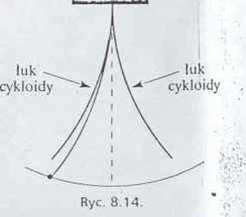
Wahadło cykloidalnc przedstawia rysunek 8.14. Nitka z kulką odchyla się i przylega do ścianki wygiętej jak luk cykloidy. Kulka będzie też poruszała się po luku o kształcie cykloidy Okres wahań wahadła cykloidalnego wyraża się wzorem:

R

S’

R - promień kola, którego punkt brzegowy zakreśli! cykloidę.

I ml? 6 JŁinaL

Okres drgań wahadła jest taki sani, jak w przypadku, gdy oś obrotu przechodziła przez koniec pręta (zad. 2.16). Punkt, przez który teraz przechodzi oś obrotu, nazywamy środkiem wahań wahadła. Środek wahań można określić jako punki odległy od poprzedniej osi obrotu o długość zredukowaną wahadła fizycznego.

Możemy więc bez zmiany okresu obrócić wahadło i spowodować jego wahanie dookoła nowej osi, przechodzącej przez środek wahań względem osi pierwotnej. Nowy środek wahań

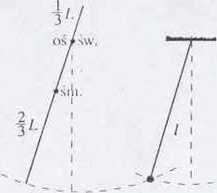
Ryc. 8.16