wah2

• ■ ■ O

Szukane: T- ?

VIII. Ruch drgający

2.8. Dane:

a. 1

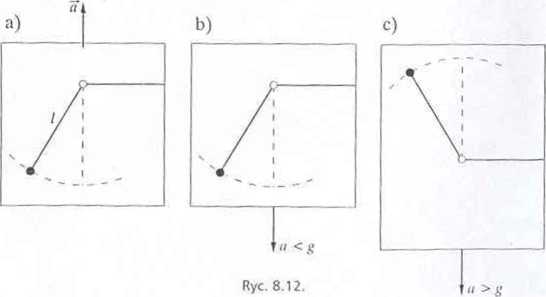
a)    Gdy kabina wznosi się z przyspieszeniem, do ciężaru kulki wahadła dodaje się sita bezwładności (ryc. 8.12a). Siła wypadkowa F = Q+ ma = mg+ m-a-m (.?+«),

^T=2nJg + “ '

b)    Gdy kabina opada, ale wolniej niż podczas spadania swobodnego, ciężar kulki jesi pomniejszony o silę bezwładności (ryc. 8.12b). Wypadkowa siła F= Q — ma = mg- ma = m(g- a),

c)    Gdy kabina zbliża się do Ziemi pionowo z przyspieszeniem a' > g\ lo siła bezwładności ma wartość większy od wartości ciężaru kulki (ryc. 8,l2c). Siła wypadkowa ma wartość F= ma — Q = ma -m (a -g),

I

a-g

!• i*

Wahadło będzie się wahało przy przeciwległej ścianie kabiny, która w przypadkach a) i b) była sufitem. Teraz swobodne, nieprzymocowane ciała będą naciskać na tę ścianę siły o wartości m(a-g). Kosmonauta będzie mógł chodzić po tej powierzchni jak po podłodze.

2.9. Dane:

Szukane: T- ?

h = 277 km, / = 25 cm= 0,25 m

- n m _ a. m •*> 2 “ ”    ⁿ ° '2

/?,,= 3400 km, M_m = 6,7- I0³³kg

Gdy statek kosmiczny zbliża się do Ziemi ruchem przyspieszonym i a < wówczas mamy sytuację taką, jak w rozwiązaniu b) zadania 2.8.

^r=27t/^Ś⁼⁶-²⁸/^li^⁼¹-^81s

W pobliżu Marsa, na wysokości 277 km, przyspieszenie grawitacyjne wynosi:

W tym przypadku a >g _ir Wahadło będzie się zachowywać tak, jak w rozwiązaniu c)

zadania 2.8.

Ściana kabiny, która w pobliżu Ziemi była podłogą, teraz, w pobliżu Marsa, jest sufitem.

2.10.    W sztucznym satelicie wszystkie ciała są nieważkie. Każde z nich obiega Ziemię po własnej orbicie, nie naciskając na ścianę kabiny ani na siebie nawzajem. Tory tych ciał i statku są wzajemnie równolegle. Sita grawitacyjna działa na ciała i na cały statek kosmiczny i powoduje jednakowe zakrzywienia torów. Wszystkie te ciała mają w każdym momencie jednakowe szybkości, jeśli są względem kabiny nieruchome. Zakładamy, że kulkę wahadła w przestrzeni kabiny umieszczono tak, by była nieruchoma względem ścian. Ponieważ nie występuje siła naprężająca nić wahadła, więc nie występują wahania. Kulka utrzymuje się w powietrzu, a nić jest „poskręcana” i nienaprężona.

2.11.    Ze względu na dużą gęstość żelaza w porównaniu z gęstością aluminium ciężar kul

ki żelaznej jest prawie trzykrotnie większy od ciężaru kulki aluminiowej. Zauważmy jednak, że we wzorze na częstotliwość drgań wahadła nie występuje ani masa kulki, ani jej ciężą i /=    J j. Zatem częstotliwość drgań nie zależy od ciężaru kulki.

Obie kulki będą miały tę samą częstotliwość drgań. Sytuacja się zmieni, gdy pod kulkami znajdzie się magnes. Pole magnetyczne będzie działać na kulkę żelazną pionowo w dól. Kulka żelazna zostanie więc poddana działaniu większej siły niż kulka aluminiowa. Częstotliwość drgań kulki żelaznej będzie większa niż aluminiowej.

/•'-silą, z jaką pole magnetyczne, działa na kulkę żelazną.

Szukane:

I =■> l = ■>

'l •'    ¹ 2

/,= l A/ = jj 0,2 m = 0,225 m = 22.5 cm

/_} = /₁- A/ = 22.5 cm - 20 001= 2.5 cm = 0,025 m

?n7