Untitled Scanned 46 (3)

którego rozwiązanie daje następujące wartości niewiadomych:

X₁ = 0,09524a£/ N; X₂ = — 0,03175a£7 N ;    X₃=0,00926aEJ N.

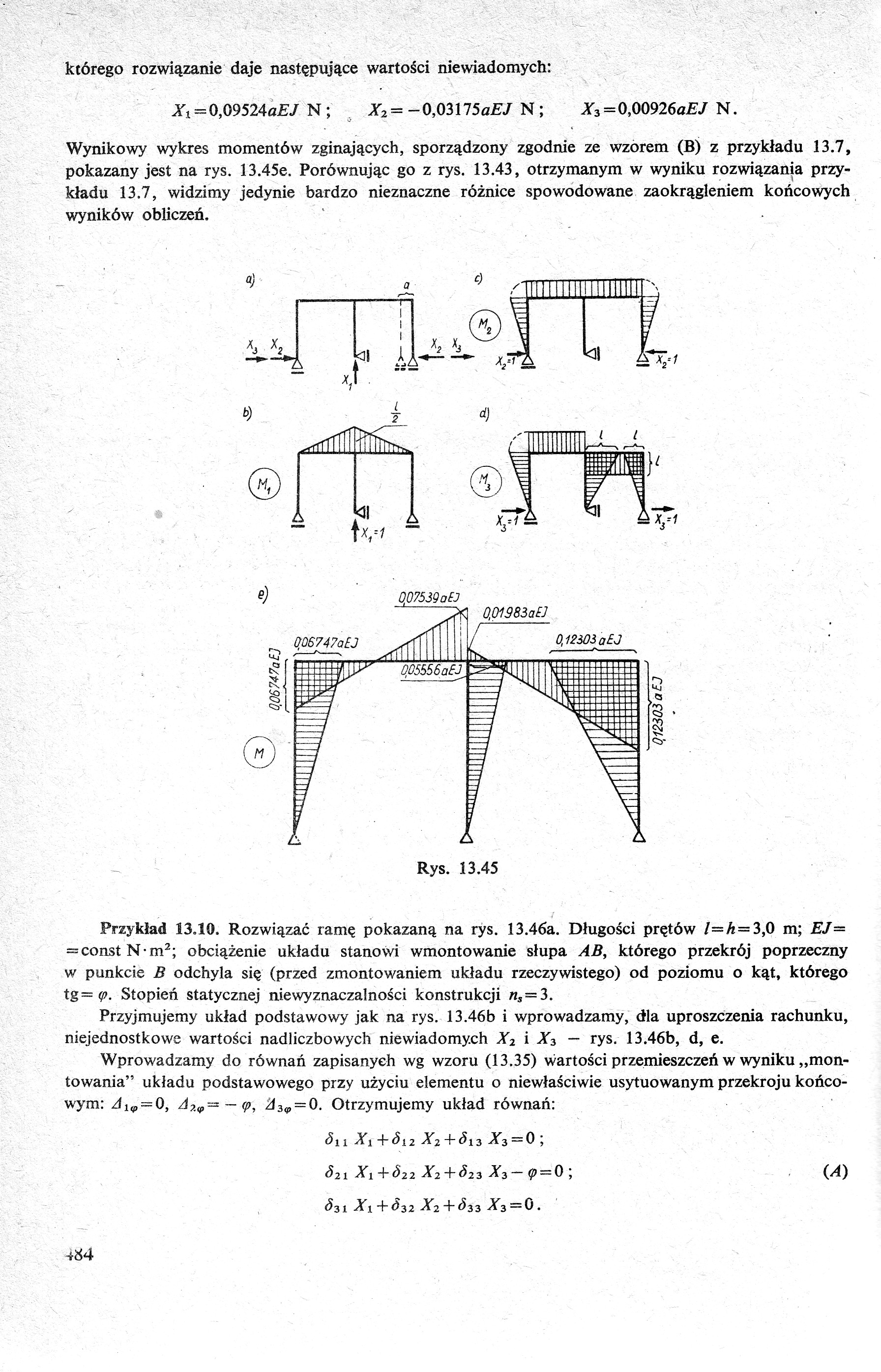
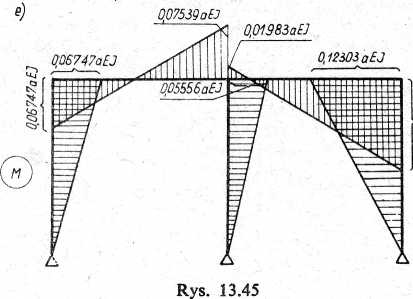
Wynikowy wykres momentów zginających, sporządzony zgodnie ze wzorem (Bj z przykładu 13.7, pokazany jest na rys. 13.45e. Porównując go z rys. 13.43, otrzymanym w wyniku rozwiązania przykładu 13.7, widzimy jedynie bardzo nieznaczne różnice spowodowane zaokrągleniem końcowych wyników obliczeń.

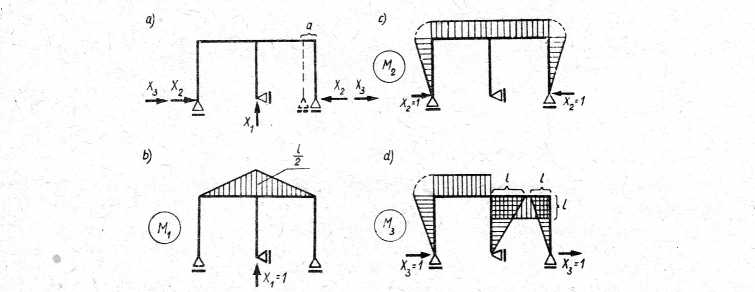
Przykład 13.10. Rozwiązać ramę pokazaną na rys. 13.46a. Długości prętów l=h = 3,0 m; EJ— = const N-m³; obciążenie układu stanowi wmontowanie słupa AB, którego przekrój poprzeczny w punkcie B odchyla się (przed zmontowaniem układu rzeczywistego) od poziomu o kąt, którego tg =<p. Stopień statycznej niewyznaczalności konstrukcji n_s — 3.

Przyjmujemy układ podstawowy jak na rys. 13.46b i wprowadzamy, dla uproszczenia rachunku, niejednostkowe wartości nadliczbowych niewiadomych X₂ i X₃ — rys. 13.46b, d, e.

Wprowadzamy do równań zapisanych wg wzoru (13.35) wartości przemieszczeń w wyniku „montowania” układu podstawowego przy użyciu elementu o niewłaściwie usytuowanym przekroju końcowym: A_lv = 0, A_2v——tp, ił_3w = 0. Otrzymujemy układ równań:

<5i i Xi +S_i2 X₂1^-ńi3 X₃ — 0 ;

(A)

S₂₂ X₂ 4- ó₂₂ X₂ -f~ S₂₃ X₃ — (jj — 0 ; S31 Xl +<5₃2 X₂ + f5₃₃ X₃ — 0.