41341 Untitled Scanned 46

- 92 -

Wzbudzenia przerzutników mają więc'postać

^wo	- Q.,-c	^zo	■ Q^*x*a*c
"1	- Q2*^d	^Z1	■ Q2'^c
^w2	- $0-b	^Z2	- V®

Ponieważ w cyklu pracy sygnał e przyjmuje wartość 1 tylko jeden raz, przy czym wtedy Q_q - 1, funkcję z₂ można uprościć do postaci

z₂ - e

Schemat układu, realizującego uzyskane funkcje wyjść i funkcje wzbudzeń pokazano na iys.3-31a. a)    fej

%. o

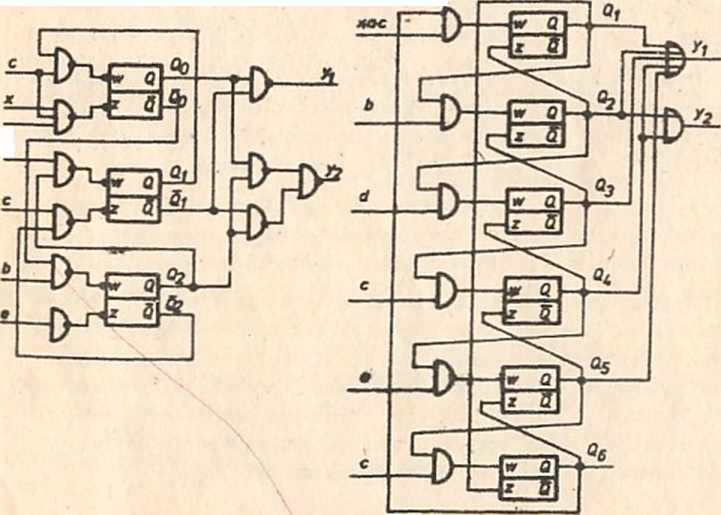
Rys.3.31. Rysunek do przykładu 3: a) układ sterujący wykorzystujący kod pseudopierścieniowyj b) układ sterujący wykorzystujący kod "1 z 6"

W procesie projektowania układów o nierozgałęzionych programach pracy, podobnie Jak w przypadku układów o programach rozgałęzionych, Jednym z podstawowych zadań Jest dobór właściwego kodu. Rodzaj kodu ma wpływ na liczbę elementów pamięciowych, złożoność funkcji wzbudzeń oraz złożoność funkcji wyjść. W celu wyeliminowania wyścigów stosuje się kody ze stałym odstępem, np. kody pseudopierścieniowe lub kody Graya. Pełna ocena wariantów rozwiązań danego układu, uzyskanych w wyniku zastosowania różnych kodów, możliwa Jest dopiero po wykonaniu projektów tych wariantów. Ponieważ dobór optymalnego kodu dla danego zadania metodą prób Jest uciążliwy,, często rezygnuje się z poszukiwania takiego rozwiązania. Dlatego też istotne znaczenie ma wstępna ocena przydatności danego kodu.

Na przykład, w przypadku sześciu stanów wewnętrznych przyjęcie kodu pseudopierścieniowego eliminuje konieczność stosowania przejść cyklicznych, występującą w przypadku użycia kodu Graya. W układach o ośmiu stanach wewnętrznych zarówno kod pBeudopierścieniowy Jak i kod Graya umożliwiają realizację cyklu pracy bez przejść cyklicznych. Zastosowanie przy ośmiu stanach wewnętrznych kodu pseudopierścieniowego wymaga użycia czterech przerzutników, podczas gdy w przypadku kodu Graya tylko trzech. Jednakże kod pseudopierścieniowy umożliwia zwykle uzyskanie prostszej funkcji przejść.

Należy zwrócić uwagę na tc, że w niektórych przypadkach, szczególnie kiedy w każdym z n taktów cyklu pracy pracuje inny element wykonawczy, korzystne może być przyjęcie kodu "1 z n", pomimo nieminimalnej liczby elementów pamięciowych. Rozwiązanie takie prowadzi do uzyskania jednakowej struktury układu sterującego dla różnorodnych zadań sterowania. Stwarza więc możliwość produkowania gotowych układów sterowania, wymagających Jedynie odpowiedniego dołączenia sygnałów wejściowych i wyjściowych. Przykład takiego rozwiązania, zastosowanego do realizacji rozważanego zadania, pokazano na rys.3.31b.

Układy sekwencyjne pracujące w kpdzie "1 z n" nazywane są rozdzielaczami sterującymi.

Przykład 4

Zaprojektować układ, którego sygnały wyjściowe reprezentują przedstawioną w kodzie Graya liczbę impulsów wprowadzanych