Untitled Scanned 57 (2)

60

GEOMETRIA ANALITYCZNA

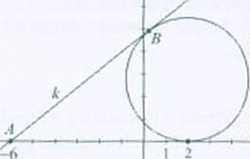
376. Okrąg przedstawiony na rysunku jest styczny do osi OX w punkcie (2. 0). a prosta k przechodzi przez punkt A = (-6, 0) i jest styczna do okręgu w punkcie />.

a)    W Jaką długość ma odcinek AB'!

b)    Znajdź równanie stycznej A wiedząc dodatkowo, żc punkt

A znajduje się w^r odległości 6V2 od środka okręgu.

377. Znajdź równania stycznych do okręgu u - l)² + (y- 1)^: = 5 poprowadzonych z punktu A -(2,0).

378. Znajdź równanie prostej równoległej do prostej o równaniu 3.v + 4y + 1 = 0 i stycznej do okręgu o równa-

niu x~ + y' - 4.v - 2y + 4 = 0.

379. R Dla jakich wartości parametru m rów nanie X² +y² - 2mx - nr + 2m = 0 opisuje okrtjg styczny do prostej o

równaniu x = 4?

380. Znajdź te wartości parametru w. dla których prosta y=x+m ma dwa punkty w spólne z okręgiem jr+y^:=2.

382. Napisz równanie okręgu przechodzącego przez punkt M = (0, I) i stycznego do dwóch prostych o równaniach x + y - 2 = 0 i x + y +3 = 0.

383. - R Znajdź współrzędne śrcxlków okręgów' stycznych do prostych u równaniach .r i 2v + 9 = 0 i 2.x - y- 2 = fi

i przechodzących przez początek układu współrzędnych.

384. W Dany jest okrąg o środku w punkcie S = (~4. 7) i promieniu długości <5. Prosta A przechodzi przez punki A = ((). 4) i przecina dany okiąg w punktach K i L. Oblicz iloczyn długości odcinków AK i AL

TRÓJKĄT

385. Punkty /t = ( 1. 2), B=l 13. 4) i C=(7, 10) są wierzchołkami trójkąta.

a)    Oblicz długość boku BC.

b)    Znajdź, równanie prostej zawierającej bok BC.

c)    Znajdź równanie prostej zawierającej wysokość poprowadzoną /. wierzchołka A.

386. Wierzchołkami trójkąta ABC są punkty A = (-3. 0), B = (1.3) i C = (-1.4).

a)    Oblicz długość wysokości opuszczonej z w ierzchołka C.

b)    Oblicz pole trójkąta ABC.