Image5 (56)

100 Rozwiązania zadań ze zbioru "MENDLA"

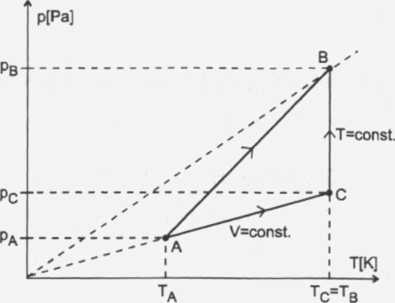
Na wykresie pokazano trzy izochory tej samej nasy gazu, więc z równaniąT'''' doskonałego mamy:

100 Rozwiązania zadań ze zbioru "MENDLA"

PA • Va Ta

PB • VB

Tb

Z rysunku odczytamy, że PB • Va _ PB • Vb Ta Tb Va Vb    _/t

Ta ~ Tb    ^/Ta

Va = Vb • ^

Tb

Z wykresu odczytamy również zależność:

Ta <Tb/ : Tb Ta

skąd =- < 1, co oznacza,

i B

że również Va < Vb.

Z równania gazu dla stanów B i C otrzymamy: PB • Vb pc • Vc Tb " T_C ’

Stąd po podstawieniu:

PB • Vb pc • Vc T_C

stąd

Pa = Pb

/: Pb

lecz z wykresu mamy: Tb = Tc

Tc

PB • Vb = pc • Vc

/• Tc

/: PB

V_B = V_C■^

PB

Z wykresu widać, że Pb > pc /: Pb

np

stąd — < 1, co oznacza, że również zachodzi relacja: PB

Vb < Vc

Ostatecznie otrzymamy:

Va < Vb < Vc

Odp.: Najmniejszą objętość ma gaz w stanie A , a największą w stanie C.

Zadanie 609 str.122

Szukane:

Czy objętość gazu wzrosła, czy zmalała?

Gaz jest ogrzewany, więc kierunek procesu zaznaczony na rysunku (strona 101) j^est zgodny z rzeczywistym od A —> B.

Zauważmy, że punkty A i B leżą na różnych izochorach (różne ciśnienia). Przejście ze stanu A do B można zrealizować po innej drodze. Najpierw ze stanu A do C przy stałej objętości, a następnie ze stanu C do B przy stałej temperaturze, ale przy wzroście ciśnienia od wartości pc do wartości Pb. Skoro przy wzroście ciśnienia temperatura jest stała, to znaczy, że objętość gazu musi się zmniejszyć.

Odp.: W naszym procesie objętość maleje.

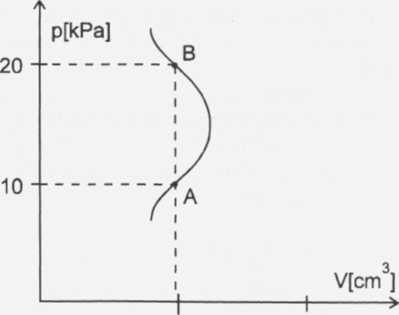
Zadanie 610 str.122

Dane:    Szukane:

Ti = 300 K    T_b = ?

Pa • Tb = pb-Ta /: pa

50

100

Z wykresu odczytujemy:

Pa = 1OkPa Pb = 20kPa

Ponieważ Va =Vb, więc gaz ze stanu A można przeprowadzić do stanu B izochorycznie, czyli zgodnie z prawem Charles^ mamy:

PĄ₌ PB Ta Tb

Tb =

PB • Tą

Pa