image 4

OBLICZENIE SKUTECZNEG( WZMOCNIENIA NAPIĘCIOWEGO

Dla zakresu średnich częstotliwości uproszczony schemat umożliwiający obliczenie przedstawiono na rys. 4.6. Powstaje on przez uproszczenie rys. 4.5 w następujący sposób:

a) pojemności C,, C₂, C_E zostają zastąpione zwarciami, gdyż ich reaklancje pojemnościowe X_cl, X_C2, X_CE są znacznie mniejsze niż rezystancje widziane z ich zacisków;

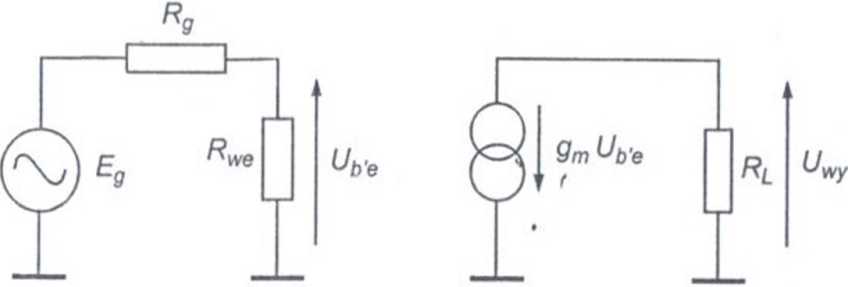
Rys. 4.6. Uproszczony schemat wzmacniacza dla zakresu średnich częstotliwości

b)    pojemności C_e, C, zastępuje się rozwarciami, gdyż reaktancje tych pojemności X_Ce, X_Cj_c są bardzo duże w porównaniu z rezystancjami na ich zaciskach; wynika to z bardzo małych wartości tych pojemności;

c)    rezystancja R_L jest równoległym połączeniem R_c i R_Q, gdyż reaktancja

*C2 * o;

d)    rezystancja wejściowa R_we = R_g\r_b._e, gdzie: R_B =    r_b,_e = P₀r_ei),,

‘Pr    kT

^reb' = T’ ^(pr⁼ —i

^    q    •    j

^e)    8_m jest transkonduktancją tranzystora: g = —.

<P_r

Na podstawie schematu z rys. 4.6 można obliczyć skuteczne wzmocnienie napięciowe dla zakresu średnich częstotliwości:

^us 0

U

wy

-R

we

8

^Rwe ⁺ r₈

Jeżeli obliczona wartość nie jest zgodna z wartością założoną, należy powrócić do punktu 2, zmienić wartość R_c lub wybrać inny punkt pracy tranzystora.

Analogicznie można wyznaczyć skuteczne wzmocnienie prądowe zastępując napięciowe źródło sygnału — prądowym. Należy wyznaczyć k:_fa0 i sprawdzić prawidłowość wzoru wiążącego k_usQ i k^:

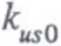
is 0

- *3

OBLICZENIE WARTOŚCI POJEMNOŚCI C,, C₂, WOŚCI DOLNEJ f_d

C_E DLA ZADANEJ CZĘSTOTLI-

W zakresie małych częstotliwości istotny wpływ na pracę układu mają pojemności C_p C₂, C_E. Schemat zastępczy przedstawiono na rys. 4.5 (ze schematu tego należy usunąć pojemności C_e i C_jc, które nie wpływają na pracę układu w tym zakresie częstotliwości). Na podstawie takiego schematu zastępczego nie da się w prosty sposób wyznaczyć dolnej częstotliwości granicznej f_d, ponieważ transmitancja jest funkcją 3-biegunową z 2 zerami w zerze i 1 zerem o niezerowej wartości (por.[l] s.155-159). Problem ten rozwiązuje się obliczając dla każdej pojemności C wartość częstotliwości dolnej wnoszonej przez nią, z pominięciem pozostałych pojemności. Podejście to powoduje powstanie błędów obliczeniowych f_d, gdyż elementy reaktancyjne przesuwają swoje bieguny i wypadkowa f_d będzie inna niż obliczona tym sposobem. Częstotliwość dolną całego układu można wtedy oszacować za pomocą wzoru:

fd ~ \fdci ⁺fdCE ⁺fdC2

gdzie: f_dcx, f_dC1, f_dCE są częstotliwościami dolnymi wnoszonymi przez poszczególne pojemności w sposób podany poniżej. Wzór ten najlepiej przybliża f_d, gdy poszczególne częstotliwości są od siebie oddalone.

W praktyce projektowej f_d wyznacza się w trochę inny sposób. Polega on na takim dobraniu składowych f_d wnoszonych przez poszczególne pojemności, aby o częstotliwości dolnej całego układu decydowała tylko jedna z nich. Najczęściej przyjmuje się f_dCE jako dominującą (gdyż daje stałą czasową z najmniejszą rezystancją), natomiast dla pozostałych f_dCl i f_dc2 dobiera się takie C, i C₂, aby f_dci i f_dcl były np. 10-krotnie mniejsze od f_dCE. Wtedy o f_d całego układu decydować będzie f_dCE. Ponieważ ^_(3dB) = l/(2itRC), więc 10-krotne zwiększenie wartości pojemności C powoduje 10-krotne zmniejszenie f_d. Sposób wyznaczania poszczególnych f_d podano poniżej:

a)    należy zastąpić zwarciami wszystkie pojemności z wyjątkiem tej, dla której wyznacza się f_d\

b)    patrząc z zacisków tej pojemności w stronę reszty układu należy określić rezystancję widzianą z jej zacisków;

c)    wyznaczyć stałą czasową x = RC, gdzie R oznacza rezystancję wyznaczoną w punkcie b);

d)    obliczyć częstotliwość dolną f_d za pomocą wzoru: f_d(3 dB) = -.

'    2 Ti RC

%

Zgodnie z przedstawionym algorytmem zostaną wyznaczone częstotliwości f_d związane z poszczególnymi pojemnościami:

67