img452 (2)

C)/(x) = |x| \ x₀ = 0; d)/(x) = |x|, x₀ = O.

Ad a) Dziedziną funkcji / jest zbiór R, a więc funkcja jest określona w każdym otoczeniu punktu x₀ = 1. Niech b będzie dowolną liczbą różną od O. Oczywiście x₀ + h e R. Mamy

/(xo + b) = /(1 + b) = (1 + b)² + 3(1 + h) - 2 = b² + 5b + 2 oraz

/(*>) =/(1) =2,

skąd

lim

h-»0

/(i +h)-m

= lim

ń-> o

(b² + 5h +2) h

-i = lim ^\⁺⁵⁾-

/i—>o    h

= lim (h + 5) = 5.

A więc istnieje /'(1) (i /'(1) = 5), zatem ta funkcja jest różniczkowalna w punkcie x₀ = 1.

Ad b) Funkcja ta jest określona w każdym otoczeniu punktu x₀ = -1, ale w lewostronnym sąsiedztwie tego punktu określona jest innym wzorem niż w prawostronnym sąsiedztwie. Należy w takim przypadku obliczyć pochodne jednostronne w tym punkcie i, jeśli one są skończone, sprawdzić, czy są sobie równe. Aby obliczyć pochodną prawostronną w punkcie x₀ = -1, załóżmy, że h jest dowolną liczbą dodatnią. Wtedy Xq -h h ⁼ — 1 + h > — 1,

zatem

/(x₀ + h)= /(—1 + h) = 4[(-1 + b) + 1 ]² = 4b² (przy obliczaniu wykorzystaliśmy drugi - „dolny" - wzór, gdyż argument funkcji jest liczbą większą od -1). Ponadto /(x₀) = /(-1) = 0, dlatego

lim

/i->0

-ł-

/H + h) -f (-1) h

= lim

/)—>o

+

4h²~0

h

= lim ₊(4b) = O.

k_vn^+v 7

Zatem /'₊(1) = O.

Jeżeli teraz założymy, że h jest dowolną liczbą ujemną, to Xq + h = — 1 + h < — 1,

zatem

/(xo + b) = /(-1 + b) = [(-1 + b) + 1]³ = b³ (dlaczego?). Oczywiście, jak poprzednio, /(—1) = O, dlatego

«M /’ ( 1) = 0.

Obie pochodne jednostronne istnieją i są sobie równe, co oznacza, że ta funkcja jest różniczkowalna w punkcie x₀ = -1 (i /'(-1) = O).

Ad c) Funkcja ta jest określona w każdym otoczeniu punktu x₀ = O, ale w lewostronnym sąsiedztwie tego punktu określona jest innym wzorem niż w prawostronnym sąsiedztwie, zgodnie bowiem z definicją wartości bezwzględnej mamy

JM)^3.	jeżeli x < 0
/w = ,
[ X^3,	jeżeli x > 0
f-X^3,	jeżeli x < 0
/W = 1 ,
L x^3,	jeżeli x > 0.

Należy więc zbadać istnienie pochodnych jednostronnych i ich równość. Mamy:

lim

h-> o'

/(°- +{?! -/(°> ~ |_im !?!■₌n_m (,2=o, ^K    h->o⁺ h    h-> o⁺

oraz

lim    ^ = lim = lim (-h²) = 0,

/t->0~    h    h^yO~ h h-+0

a więc pochodne jednostronne są sobie równe, zatem funkcja jest różniczkowalna w punkcie x₀ = 0 (i /'(O) = 0).

Ad d) Podobnie jak w punkcie poprzednim zbadamy istnienie pochodnych jednostronnych i ich ewentualną równość. Mamy

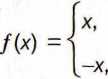
/(-1 + ft) — /(—1) __Nm ^-0

lim •'' I' *'    ' = lim

At -+o    h    h->cr

= lim h² = 0,

b->cr

jeżeli x > 0 jeżeli x < 0

lim ,

h~* o^-'

/(O + W^/jp)    ₌

h    h->o⁺h

lim

h->0'

/(O + h)

h

₌ lim

h—>o~

-h_ h

= -1.

Obie pochodne jednostronne istnieją, ale nie są sobie równe, więc funkcja nie jest różniczkowalna w punkcie x₀ = 0 (czyli /'(O) nie istnieje).