img465 (3)

noległość siecznej i stycznej oznacza równość Ich współczynników kierunkowych. Współczynnikiem kierunkowym siecznej jest liczba ^ ^    nato

miast współczynnikiem kierunkowym stycznej liczba /' (c). Mamy więc:

Ą TWIERDZENIE 1.(Lagrange a)

Jeżeli funkcja / jest ciągła w przedziale domkniętym (a, b) oraz różniczkowal-na w przedziale otwartym (o, b), to istnieje taka liczba c e (a, b), dla której prawdziwa jest równość:

f'(_c\ = f(^b) ~ /(^g)

^JK) b-a '

Czasami wygodnie jest tezę tego twierdzenia zapisywać w postaci:

f(b)=f(a)+f(c)-(b-a).

Dowód tego twierdzenia pominiemy.

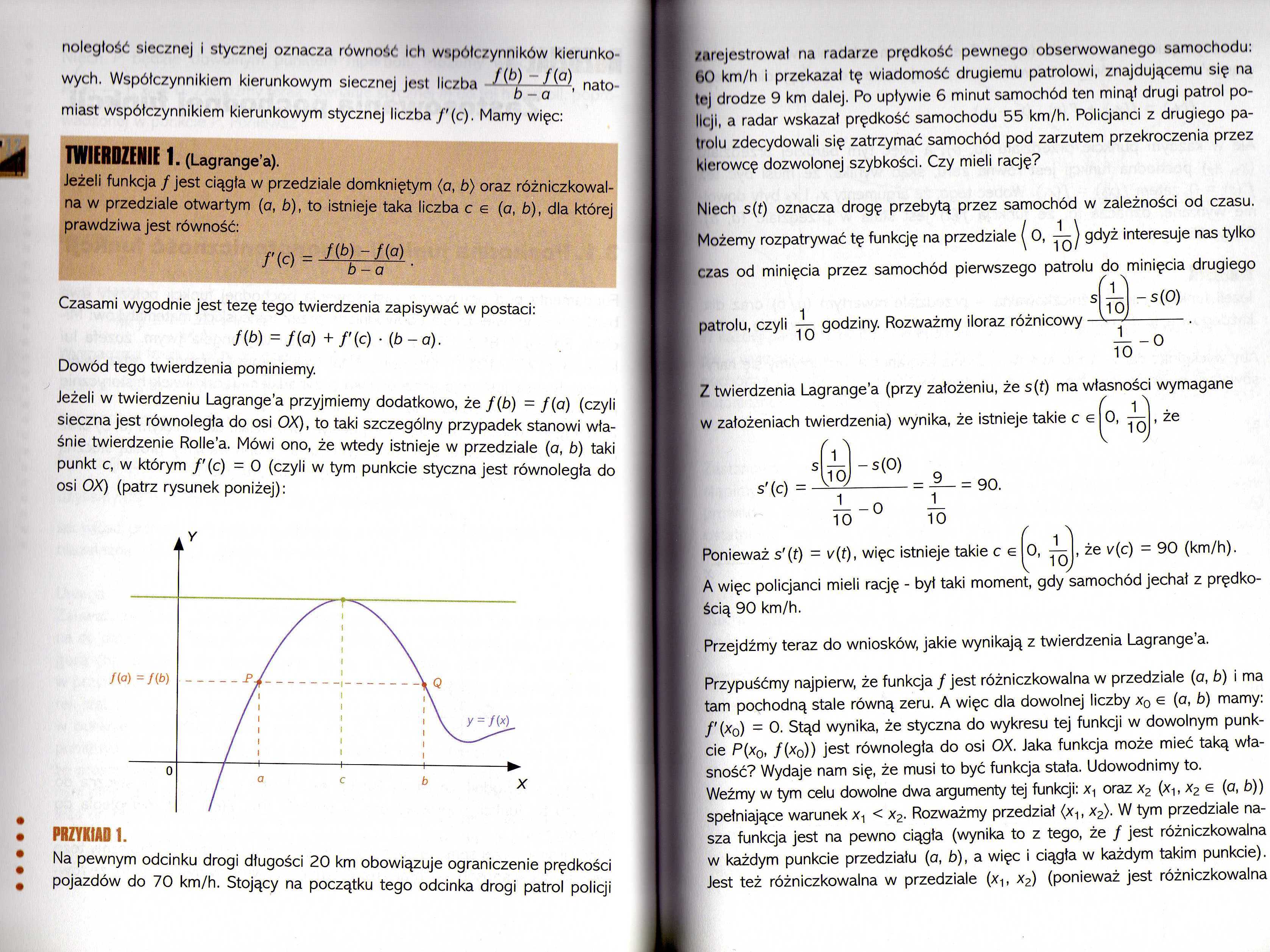
Jeżeli w twierdzeniu Lagrange’a przyjmiemy dodatkowo, że /(b) = /(a) (czyli sieczna jest równoległa do osi OX), to taki szczególny przypadek stanowi właśnie twierdzenie Rolle’a. Mówi ono, że wtedy istnieje w przedziale (a, b) taki punkt c, w którym /' (c) = O (czyli w tym punkcie styczna jest równoległa do osi OK) (patrz rysunek poniżej):

mmm 1.

Na pewnym odcinku drogi długości 20 km obowiązuje ograniczenie prędkości pojazdów do 70 km/h. Stojący na początku tego odcinka drogi patrol policji

zarejestrował na radarze prędkość pewnego obserwowanego samochodu: 60 km/h i przekazał tę wiadomość drugiemu patrolowi, znajdującemu się na lej drodze 9 km dalej. Po upływie 6 minut samochód ten minął drugi patrol policji, a radar wskazał prędkość samochodu 55 km/h. Policjanci z drugiego pa-Itolu zdecydowali się zatrzymać samochód pod zarzutem przekroczenia przez kierowcę dozwolonej szybkości. Czy mieli rację?

10

Niech s(t) oznacza drogę przebytą przez samochód w zależności od czasu. Możemy rozpatrywać tę funkcję na przedziale ( 0, gdyż interesuje nas tylko czas od minięcia przez samochód pierwszego patrolu do minięcia drugiego

s(0)

o

patrolu, czyli ^ godziny. Rozważmy iloraz różnicowy

10

Z twierdzenia Lagrange'a (przy założeniu, że s(t) ma własności wymagane

, że

w założeniach twierdzenia) wynika, że istnieje takie c e -s(0)

s'(c) - ^v10y

10

0

= JL_ = 90. 10

v ¹⁰;

°’ To

, że v(c) = 90 (km/h).

Ponieważ s'(t) = v(t), więc istnieje takie c

A więc policjanci mieli rację - był taki moment, gdy samochód jechał z prędkością 90 km/h.

Przejdźmy teraz do wniosków, jakie wynikają z twierdzenia Lagrange’a.

Przypuśćmy najpierw, że funkcja/jest różniczkowalna w przedziale (a, b) i ma tam pochodną stale równą zeru. A więc dla dowolnej liczby x₀ e (o, b) mamy: f'(xo) = 0. Stąd wynika, że styczna do wykresu tej funkcji w dowolnym punkcie P(x₀, /(x₀)) jest równoległa do osi OX. Jaka funkcja może mieć taką własność? Wydaje nam się, że musi to być funkcja stała. Udowodnimy to.

Weźmy w tym celu dowolne dwa argumenty tej funkcji: X-, oraz x₂ (x_1f x₂ e (a, b)) spełniające warunek x< x₂. Rozważmy przedział (x_1t x₂). W tym przedziale nasza funkcja jest na pewno ciągła (wynika to z tego, że / jest różniczkowalna w każdym punkcie przedziału (a, b), a więc i ciągła w każdym takim punkcie). Jest też różniczkowalna w przedziale (x_1t x₂) (ponieważ jest różniczkowalna