instalacje112

4. TEORIA SILNIKÓW SKOKOWYCH 106

Równanie (4.27) może być uproszczone przez podstawienie /₂_₀ = = /j_o = / oraz założenie, że początkowy moment obciążenia M_t0 — 0.

Posługując się tymi uproszczeniami, otrzymano; cos 0_O—sin 0_o — 0 lub 9_a = 45°. Wtedy równanie (4.27) można zapisać w postaci

R + Łs

[a£^₂(s)+

A 6(s) =

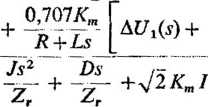
(4.28)

Przy zakłóceniach momentu obciążenia wokół punktu pracy po wykonaniu skoku i początkowym momencie obciążenia równym zeru, odpowiedź silnika ogranicza się do wyrażenia

yAM_t(_S)Z_r

(4-29)

Wyrażenie to jest bardzo użyteczne, gdyż odpowiedź silnika skokowego jest opisana jako funkcja częstotliwości drgań własnych, współczynnika tłumienia i stałej sztywności mechanicznej, te zaś parametry mogą być łatwo określone eksperymentalnie.

Częstotliwość drgań własnych i współczynnik tłumienia zlinearyzowanego modelu silnika skokowego o magnesach trwałych mogą również być wyznaczone przez rozpatrzenie małych zmian A0 w stosunku do punktu równowagi.

Rozpatrując zlinearyzowane równanie dla punktu równowagi stabilnej, przy stałym prądzie stojana i momencie obciążenia równym zeru, uzyskuje się jego uproszczenie do postaci

(4.30)

Równanie (4.30) może być użyte do wyznaczenia częstotliwości drgań własnych i współczynnika tłumienia zlinearyzowanego modelu

dla stabilnego punktu równowagi. Przeprowadzono doświadczenie dla dwu silników. W każdym z nich zasilono oba uzwojenia, wirnik wyprowadzono z punktu równowagi, symulując małą zmianę A0. Jako przetwornik położenia zastosowano potencjometr, odpowiedź rejestrowano na oscyloskopie. Zmierzona częstotliwość drgań własnych wyniosła 420 rad/s dla jednego z silników i 860 rad/s — dla drugiego, współczynniki tłumienia zaś odpowiednio 0,125 oraz 0,21.

Model hybrydowego silnika skokowego

Modelem hybrydowego silnika skokowego posłużyli się D WJ. Pulle i A. Hughes [86] przy analizie pracy silnika zasilanego napięciem

0    stałej wartości. Celem było znalezienie relacji pomiędzy parametrami silnika i jego wyjściową mocą mechaniczną oraz przedstawienie wyników w postaci ogólnej, przydatnej dla wszystkich silników hybrydowych. Ujęcie przedstawione w pracy [86] różni się od dotychczasowych tym, że skupia uwagę na mechanicznej mocy wyjściowej, nie zaś na momencie, jak to czyniono dotychczas, stojąc na stanowisku, że najistotniejsze znaczenie mają przemiany energii, a ponadto posłużono się wykresem kołowym Blondella, używanym zasadniczo do analizy maszyn synchronicznych

1    tylko sporadycznie w przypadku silników skokowych.

Jako podstawę do stworzenia modelu przyjęto hybrydowy silnik skokowy pokazany na rys. 1.6. Poczyniono następujące założenia upraszczające: przyjęto, że indukcyjność własna jest niezależna od położenia wirnika; prądy wirowe i efekt nasycenia pominięto. Ponadto, z uwagi na konfigurację uzwojeń, indukcyjność wzajemną pominięto. Te założenia upraszczające są typowe dla tego rodzaju silników i prowadzą do modelu

Rys. 4.7. Model dwubiegunowego hybrydowego silnika skokowego (wg [861)