instalacje116

4. TEORIA SILNIKA SKOKOWEGO 114

gdzie

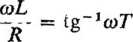
(4.55)

Podstawiając |/₂| z równania (4.42) i wprowadzając parametr k_p, współrzędne punktu na krzywej roboczej będą określone wzorami

1 kp coT		~ 1 - co^2T^2 "
_ 2 V f + <w^2r^2 _		l+co^2T^2
1 kp coT ~		2o)T
~2 ^J l + co^JT^2 _	1 +w^2T^2

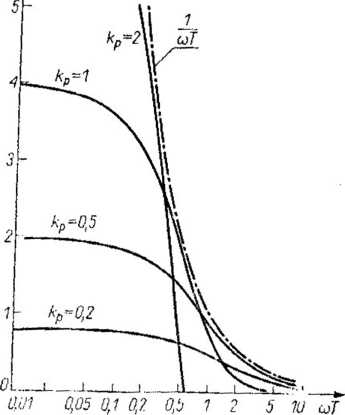
Równania (4.56) i (4.57) umożliwiają utworzenie rodziny krzywych przy różnych wartościach parametru k_p i iloczynu coT, które pokazano na rys. 4.11. Krzywe te przedstawiają zależność pomiędzy mocą wyjściową i parametrami hybrydowego silnika skokowego.

Aby określić moc maksymalną przy danej wartości prędkości, trzeba znać moc wejściową przy nieruchomym wirniku, która wynosi U²jR. Maksymalna moc wyjściowa (100%) jest równa V²(AR i określa

1

100

1C

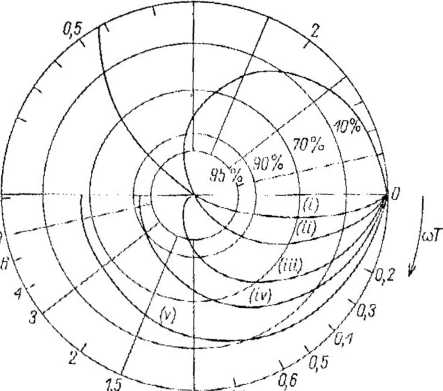
Rys. 4.11. Znormalizowane krzywe robocze silnika hybrydowego (wg [86]) (i) k_p = 2; (ii) k₀ « 1; (iii) k_p — 0,5; tjv) k_p = 0,35; (v) k_p = 0,2

p

—'^'0,6

0,8

skalę mocy na rys. 4.11. Przy znanym parametrze k_e położenie na krzywej, odpowiadające danej prędkości, jest umiejscowione na podstawie znajomości stałej czasowej T (a tym samym iloczynu oT).

Wartość parametru k_p w decydującym stopniu wpływa na charakter znormalizowanej krzywej mocy wyjściowej. Jeżeli k_p < 0,5, to maksymalna (100%) moc wyjściowa nie będzie nigdy osiągnięta, niezależnie od prędkości. Przy k_p = 0,5, osiąga się 100% mocy, lecz tylko przy nieskończenie dużej prędkości, natomiast przy 0,5 < k_p < 1 osiąga się moc maksymalną przy skończonej prędkości.

Informacje zawarte w wykresie kołowym Blondella mogą być przedstawione w postaci charakterystyk mechanicznych, wykonanych M

w relacji - ■— = f (cdT), przedstawionych na rys. 4.12. Równanie cha-

M

max

rakterystyk, otrzymane na podstawie wzorów (4.40), (4.49), (4.50) i (4.51), ma postać

]')

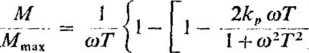
(4.58)

M

Rys. 4.12. Charakterystyki mechaniczne silnika hybrydowego

8*