instalacje120

4. TEORIA SILNIKA SKOKOWEGO 122

Równania napięć na uzwojeniach stojana

u - Rh -    - "^d/² + • £- (AW>„, cospfl) = 0    (4.63)

^LAJ-²- - ^L^AI1. + £[m_mcosj>(9-z)] = 0 (4.64)

Należy zwrócić uwagę, że ponieważ moment reluktancyjny jest w tym przypadku pomijalnie mały, wobec tego indukcyjność własną L i wzajemną M przyjęto jako zależną od kąta 0.

Równania zostaną zlinearyzowane przy założeniu, że nieznaczne zakłócenie położenia 30 (t) w stosunku do położenia równowagi jest związane z odpowiednimi zmianami prądów: 3J_k(t) oraz 31₂(t). Gdy I₀ oznacza prąd ustalony w obu pasmach, a kąt równowagi wynosi t/2, wówczas zlinearyzowane równania prezentują się następująco:

m + -^DA (50) + 2p*>P_m    N„ cos (^P2^T- j ( ) +

+p<P,„Nsm f^P2^r j (5/, -Sl₂) = 0 (4.65)

K (51,) +    (51,) +    (SI₂) -p<P_m N sin (^P-) 1 (50) = 0

(4.66)

R(5h)+ “ «/₂)+ («.)+^ATsin(^PM ^d (<50) = 0

(4.67)

Dla wygody podstawiono w dalszym ciągu: 30 — 0': 3 Ą = /j oraz Ó 1₂ = l’₂■ Rozpatrując przypadek, kiedy wirnik zostaje uwolniony ze stanu spoczynku w swoim położeniu równowagi przy kącie 0_h rozwiązanie równań (4.65), (4.66) i (4.67) w postaci operatorowej przyjmie postać

li =

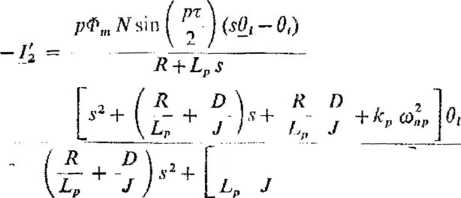
(4.68)

+

R D . _f

+ ⁱ⁰np ( 1 + /c„)

(O.,

(4.69)

gdzie:

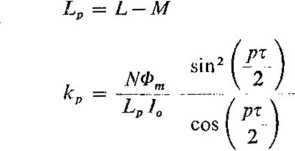
(470)

(4.71)

2p²<P,_n NI₀ cos

....

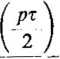
(4.72)

Przed przystąpieniem do rozwiązania równań rozpatrzmy podobne równania silnika skokowego o wirniku reluktancyjnym, którego elementarny model przedstawia rys. 4.18b.

lndukcyjności własne i wzajemne uzwojenia dwupasmowego (rys. 4.1 Sb) mają ogólną postać

L_X1 = L₀ +L_Z cos 2p0    (4.73)

L₂₂ = L0 + L2 COS 2/7 (0 - t)    (4.74)

M_i2 = - M₀+M₂co$2p( 0-~    (4.75)

Znak minus przed indukcyjnością wzajemną M₀ w równaniu (4.75) oznacza, że dodatni prąd w jednym uzwojeniu wytwarza ujemny strumień skojarzony w drugim.

Wypadkowy moment obrotowy wytwarzany przez prądy /_l oraz I₂ określa wzór

M =

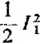
dL_n

dfl

+

1    _j2 dL₂2_

2    ² dćT

+ /i/a

ÓM₁

dO

(4.76)

Równanie ruchu

(4.77)

2 ~ + ff~ + / jP^L2 sin 2pO + / \ pL₂ sin 2p (0 — r) + + /i h 2pM₂ sin 2/?    — yj =0