14130 instalacje113

4. TEORIA SILNIKÓW SKOKOWYCH 108

pokazanego na rys. 4.7, na którym dla uproszczenia pominięto obwód pasma 2.

Każde z pasm było wzbudzane impulsami prostokątnymi napięcia w układzie bipolarnym, które są reprezentowane w analizie przez podstawową składową napięcia u(t). Rezystancja R, widoczna na rys. 4.7, jest sumą rezystancji pasma i rezystancji zewnętrznej, zwanej forsującą (patrz rozdz. 3).

W pierwszej kolejności będzie rozpatrzony silnik hybrydowy pracujący w stanie ustalonym z dużą prędkością przy danej częstotliwości zasilania. Oznacza to, że nie będzie rozpatrywane zagadnienie rezonansu przy malej częstotliwości ani też problem niestabilności przy dużych prędkościach.

Będzie rozpatrzony silnik pracujący ze stałą prędkością wirnika Q_m. Uwaga będzie skupiona na tym, jak wpływa obciążenie na wale silnika na jego pracę oraz jak parametry układu wpływają na maksymalną moc, uzyskiwaną przy danej prędkości.

Napięcie wzbudzenia u (t) jest wyrażone wzorem

u^sjlU cos (ot    (4.31)

Równanie napięć dla pasma / d^

u = Ri+~*~    (4.32)

Występująca w równaniu (4.32) wielkość zmienna W jest strumieniem skojarzonym z pasmem J, który można określić wzorem

V = Li+ N<P_m cos 0    (4.33)

Pierwszy czynnik jest związany z indukcyjnośeią własną pasma, drugi zaś zależy od strumienia <P_m magnesu trwałego i od liczby prętów /V W paśmie /.

Biorąc pod uwagę założenie o stałej prędkości kątowej Q_m, kąt będzie określony wzorem

0 = (ot —

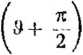
(4.34)

Kąt obciążenia jest — podobnie jak w teorii konwencjonalnych maszyn synchronicznych — kątem pomiędzy U_t oraz U w schemacie zastępczym (rys. 4.8).

o-

U

o

-o~

Zab    Ut

B

Rys. 4.8. Schemat zastępczy hybrydowego silnika skokowego

Związek częstotliwości wzbudzenia z liczbą skoków S wynika ze wzoru

tt „ co = — S 2

Podstawiając (4.33) i (4.34) do (4.32), otrzymuje się , d/ d

u — Ri+L-—h —— N4>_m cos

(4.35)

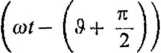
(4.36)

Rozwiązanie równania (4.36) można uzyskać przez przekształcenie w dziedzinę liczb zespolonych, za pomocą wyrażenia

x (t) = \ 2 Re [A'e^Ja,f]

które umożliwi przedstawienie równania (4.36) w postaci

(4.37)

U-Uj = (R + }(oL)I

gdzie

(4.38)

U i — 0iN4>_m e^_J3

(4.39)

Równanie (4.38) prowadzi bezpośrednio do modelu obwodu przedstawionego na rys. 4.8, w którym Z_AB jest impedancją wejściową, odczytywaną z zacisków A i B. Prąd w paśmie 2 będzie identyczny jak w paśmie 1, lecz przesunięty w czasie o kąt tu/2.

Schemat zastępczy hybrydowego silnika skokowego przedstawiony na rys. 4.8 jest zbudowany jak typowy schemat zastępczy maszyny synchronicznej z biegunami utajonymi, co wynika z poczynionych założeń upraszczających.

Maksymalna mechaniczna moc wyjściowa może być obliczona ze wzoru

Pr

> - H²

^ma* ~ ~4R

(4.40)