MATEMATYKA091

174 ID. Rachunek różniczkowy

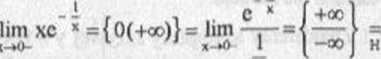
= lim-}

H *~»0-

X

I

= lim(-c *) = -cc,

Wynika stąd, źc prosta x = 0 jest asymptotą pionową (lewostronną) wykresu funkcji f.

Szukamy asymptoty ukośnej danej krzywej przy x —> +oo:

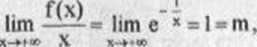
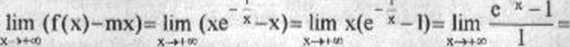
x

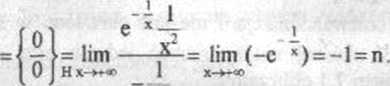
x

,2

Zatem prosta o równaniu y = x - 1 jest asymplotą ukośną danej krzywej przy x y +oo. Analogicznie otrzymujemy, że prosta y = x-l jest asymptotą tej krzywej również przy x -> -oo.

Krzywa y = f(x) ma więc asymptotę pionową (lewostronną): x = O

oraz asymptotę ukośną y ■ x-1 (przy' x -* +oc i przy x -> -oo.)

ZADANIA DO ROZWIĄZANIA

1 Wyznaczyć dziedzinę funkcji:

i na tej podstawie odpowiedzieć na pytanie: czy wykres tej funkcji może mieć asymptoty pionowe?

2. Wyznaczyć dziedzinę funkcji:    _

a)y = ln(2-x), b)y = xc^Vx*\ c) y = V9x-x^:

i na tej podstawie odpowiedzieć na pytanie: czy wykres tej funkcji może mieć asymptoty ukośne przy x -> +oc lub x —>    ^>

Znaleźć asymptoty krzywej y = y(x)»gdy:

a) y =

x -x

x²- x-2 ’

d)    y = e^2_x,

^{e) y = x + ,n}^2 j) y=Vx² -6x,

i

I) y = xe^vX,

b) y - xarctgx.

. xlnx e) y =

h)y =

I In x '

e *-x^ł

..2

k) y = x-2arclgx.

I-X*

^{c) y =} x+2^e

1-X 1 + X *

2xlnx-I

0 y = arccos

i) y =

lnx

X

1) y = xe^x"',

m)y=e^2,xx\ n) y = x-e^<x"^,,x.

Odpowiedzi

3.    a)x=2,v*x+l; b) y = -l+Jtx/2 przy x-»-ko, y = -l-xx/2 prz>‘

c) x=—2, y = 0 przy x->+oo; d) x=2, y = l; e)x=e; f)y = *'- g) x*-2, x=0 y=x, h) x=0, y = -x przy x->+x>, i) y = 2x, x= 1, j) y=-x+3 przy *-►-<*>, y = x-3 prz x-»+oc, k) y = x+ir przy x-+-ao, y = x-n przy x-*+•»,

1) y *cx+c, x = l, ł) x=0, m)x=2, y-l/c, n) y = x-l

8. BADANIE PRZEBIEGU ZMIENNOŚCI

FUNKCJI

BADANIE FUNKCJI OKREŚLONEJ WZOREM y = f(x). Badanie przebiegu zmienności funkcji (krótko: badanie funkcji) jest zadaniem złożonym, wymagającym znajomości wszystkich zagadnień rozważanych we wcześniejszych paragrafach tego rozdziału. Celem tak postawionego zadania jest uzyskanie możliwie wielu informacji o badanej funkcji - o jej monotomczności, ekstremach, wypukłości, wklęsłości - i sporządzenie wykresu z uwzględnieniem wszystkich charakterystycznych cech tej flmkcji.