MATEMATYKA095

182 ID. Rachunek różniczkowy

pochodnej (można sprawdzić, że f'(x)-»+oc przy x->l, styczna do wykresu jest wtedy prostopadła do osi 0x). Wykres funkcji f przedstawia rysunek 8.3.    ■

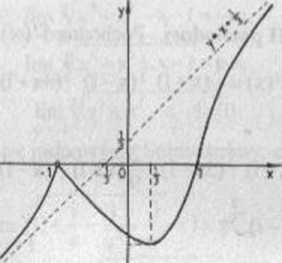
Rys 8.3

PRZYKŁAD8.4 Zbadamy przebieg zmienności funkcji f(x) = lnjsin x|.

(1)    Dziedzina. Granice. Asymptoty. Funkcja f określona dla xeD = {xeR: x*kx, keC}. Zauważmy, że funkcja ta jest okresowa o okresie równym K. Istotnie dla każdego x € D mamy:

ln|sin(x + k)|= ln|—sin xj= ln|sin x|.

Wystarczy więc zbadać funkcję f na przedziale (0,7t). Obliczamy granice: lim ln|sin x|= -oo,    lim ln|sin x|= -co.

* »<>•    *-»n-

Proste x = 0 i x = tc są asymptotami pionowymi wykresu.

(2)    Badanie I pochodnej. Ponieważ dla x e(0,7t)

ln|sin x|=lnsinx,

więc

X 6(0, Jl).

Stąd dla xe(0,łi) mamy

f'(x)>0 <?> 0<x<y,    f'(x)<0 o ~<x<n

(3)    Badanie II pochodnej. Ponieważ

f"(x) = —X€(0,7t), sin x

wiec f"(x)<0dla x z rozpatrywanego przedziału

(4)    Zestawienie wyników w tabeli.

	0		k/2		7t
f’(x)		+	0	—
f"(x)		_	_	_
f(x)	* / v	-X	max 0	j 8	■ «««?» iiiiĄw.

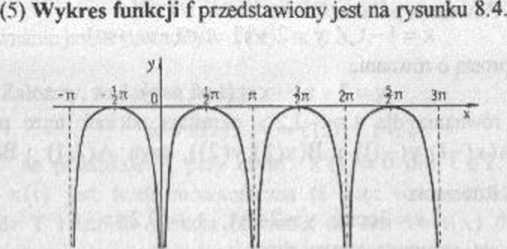
Ry s 8 4

Uwaga. Oczywiście nic zawsze wszystkie elementy badania funkcji, jakie zaprezentowaliśmy w powyższych przykładach, są łatwe (a nawet możliwe) do przeprowadzenia. Czasem pełne badanie, z uwagi na postawione pytanie w zadaniu, nie jest celowe

FUNKCJA OKREŚLONA PARAMETRYCZNIE Rozważane wcześniej przykłady badania przebiegu zmienności funkcji danej wzorem y = f(x) kończyły się naszkicowaniem wykresu tej funkcji, czyli krzywej danej tzw. równaniem jawnym y = f(x).