MATEMATYKA098

188 111. Rachunek różniczkowy'

i sporządzamy tabelę:

t	0		t:		2n
X'(t)	0	+	+	+	0
y'(0	0	+	0	—	0
x(t)	0		KU		2na
y(t)	0		2a		0

Ponieważ x'(t) * 0 dla t c (0,27t), więc równania (1) określają parametrycznie funkcję y = f(x), której pochodne f' i f" wyrażają się, zgodnie z (8 2) i (8.3), wzorami:

sin t

T(x) = -

f'(x) =

1

1 — cost’    * ^v"⁷    (1-cost)²

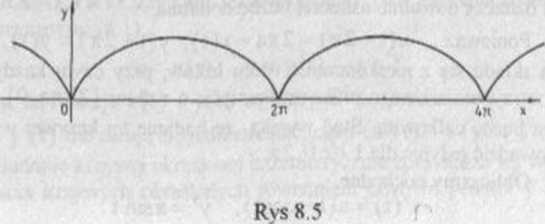
Zatem funkcja f jest rosnąca, gdy te(0,7t), malejąca, gdy t e(7c,27c), czyli funkcja f jest rosnąca dla x€(0,7ta), malejąca dla x e(7ra,27ra), a dla t = ;c, czyli x = 7ta funkcja f osiąga maksimum lokalne równe 2a

Ponieważ f"(x)<0, więc krzywda jest wklęsła na całym rozważanym przedziale.

Asymptot krzywa nie ma.

Badana krzywa (rys 8.5) nazywa się cykloidą Jest to krzywa, którą zakreśla ustalony punkt okręgu o promieniu a toczącego się (bez poślizgu) po prostej.    ■

PRZYKŁAD 8.8 Zbadamy

2 + t²

(1)

x =

l+t

2 »

y =

i + t^:

krzywą określoną równaniami t €R.

Ponieważ

limx(t)=l i Iimy(t) = +oo, limy(t) = -oc,

więc prosta x = 1 jest asymplotą pionową krzywej. Innych asymptot nic ma.

Obliczamy pochodne

x'(t)

i sporządzamy tabelę:

-2t

(l + t²)²'

y'(t)

t²(3 + t²) (l + t²)²

t	-00.......	0	.......+00
x'(t)	+	0	—
y'(t)	+	0	+
x(t)		2
y(t)	-00	0	+00

Zauważmy, że dla punktów (x,y) badanej krzywej mamy: x€(l,2>, zaś y €(-oo,+qo).

Ponieważ x'(0) = y'(0) = 0, więc punkt P_o(x(0),y(0)) = = P₀(2,0) jest punktem osobliwym krzywej. Natomiast na każdym z przedziałów: (-oo,0) oraz (0,+oo) równania (1) określają funkcję postaci y = f(x), przy czym x €(1,2) oraz

f'(x) = -it(3 ₊ t^ł). f"(x) = ^-±pL,

Stąd wynika, że dla x €(1,2) określone są dwie funkcje: y = f,(x) - malejąca i wypukła (dla t > 0 ) oraz y = f₂(x) - rosnąca i wklęsła ( dla t < 0 ). Wykorzystując wszystkie uzyskane informacje szkicujemy krzywą (rys 8.6).    ■