86715 MATEMATYKA092

176 111. Rachunek różniczkowy

Z uwagi na złożoność tego zadania przyjmujemy następujący schemat badania przebiegu zmienności funkcji;

(1) Wyznaczamy dziedzinę i granice funkcji w punktach brzegowych dziedziny. Znajdujemy asymploty wykresu.

(2)    Obliczamy I pochodną funkcji. Znajdujemy miejsca zerowe i badamy znak tej pochodnej,

(3)    Obliczamy II pochodną funkcji. Znajdujemy miejsca zerowe i badamy znak tej pochodnej.

(4) Sporządzamy tabelę - w- tabeli umieszczamy uzyskane wcześniej rezultaty i zapisujemy wnioski o monotoniczności i ekstremach (na podstawie znaku I pochodnej) oraz o wypukłości, wklęsłości i punktach przegięcia (na podstawie znaku II pochodnej).

(5)    Na podstawie informacji zawartych w' tabeli sporządzamy wykres funkcji. Wykorzystujemy przy tym także dodatkowe informacje takie jak; punkty przecięcia wykresu z osiami układu współrzędnych, parzystość lub nieparzystość funkcji.

PRZYKŁAD 8.1 Zbadamy przebieg zmienności funkcji

(I) Dziedzina. Granice. Asymptoty. Dziedziną tej funkcji jest zbiór D = (-oo_ł4)u(4,-f-oo). Obliczamy granice;

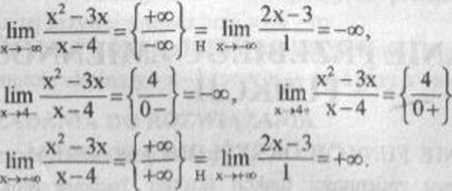
Ponieważ w punkcie x - 4 obie granice jednostronne funkcji f są niewłaściwe, więc prosta o równaniu x = 4 jest asymptotą pionową obustronną wykresu lej funkcji. Sprawdzamy, czy istnieją asymptoty ukośne tego wykresu;

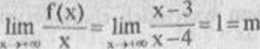
lim (f(x)-mx)- lim (-—~~x) = lim —^-r= l = n.

»>.«. x-4 x >^x-4

Łatwo sprawdzić, żc

f(v\

lim-= l~m, lim (f(x)- mx)= 1 -n.

Stąd wynika, te prosta y = x +1 jest asymptotą ukośną wykresu funkcji f w plus i w minus nieskończoności

(2) Badanie I pochodnej, Obliczamy pochodną funkcji f:

. x²-8x + 12 ^{f (x)} = ——-~2~, xeD.

(x-4)

Stąd dla x e D mamy:

f'(x) 0 <=> x²-8x + 12 = 0 o (x = 2 v x = 6), f'(x)><) <=> x²-8x + 12>0    (x<2 v x>6),

f'(x)<0 o x²-8x+12<(> o (2<x<6).

(3)    Badanie II pochodnej. Ponieważ

^xeD’

(x-4)

f"(x)/0, x€D; f"(x)>0ox>4; f"(x)<0ox<4,

(4)    Zestawienie wyników w tabeli.

X	-co.......	2		4		6	........+00
f'(x)	+	0				0	+
f"(X)	-				+	+	+
f(x)		max 1	j 8		+00	9 min	+00

Uzyskane wcześniej wyniki wpisujemy do tabeli Na podstawie znaku I pochodnej wnioskujemy o monotoniczności funkcji w poszczególnych przedziałach, a na podstawie znaku II pochodnej - o wypukłości i wklęsłości wykresu