P1020333 (2)

*klMm

1 matematyki, l rok. ZIP (*eme*tr letni j„„.

SMHHKff ^Ł 'Z⁷ " j    V

Zadanie l, Obliczyć fcas(ln.vu/.v

fi-COS X

(a-D*

/.ndanie 2. /.badać (nic obliczając!) zbieżność całki )    ..........- dx

/udanie 3. /badać zbieżność szeregu T* fi

\ ii i

/.udanie 4. Obliczyć

lim

i.v, ;,•)->( 0.01

sini.Y" - v~)

\-v²-y²

/udanie 5. Niech

/(•v. r):=

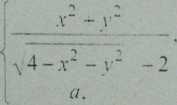
gdy (x.y i = (0.0) gdy (.y. r) = (0.0).

Dla jakiej wartości a e 1 funkcja / jest ci aula w punkcie (0.0)7

/.udanie 6. Zbadać różniczkowalność funkcji

I

j(x.y)'.-\e ^x . gclv (_v,y) ^ (0.0), w punkcie(0.0).

i 0.    gdy (,v.y) = (0,0)    jfję b^e

/udanie 7. Znaleźć punkt, w którym gradient funkcji | = In — jest równy i+j.

v

Zadanie 8. Obliczyć pochodną funkcji i = ,v w punkcie (C.l) w kierunku wektora A fi łączącego punkty A (1. -1) i B( 3.-2).

Zadanie 9. Obliczyć pole figury płaskiej ograniczonej krzywymi o równaniach r -■ :.Y" ,y - ,v 1,.V * “ V ~ i •

Zadanie 10. W\znaez.ye ekstrema lokalne funkcji j — ,v i -    \*